Inside Heat Balance[LINK]
The heart of the heat balance method is the internal heat balance involving the inside faces of the zone surfaces. This heat balance is generally modeled with four coupled heat transfer components: 1) conduction through the building element, 2) convection to the air, 3) short wave radiation absorption and reflectance and 4) longwave radiant interchange. The incident short wave radiation is from the solar radiation entering the zone through windows and emittance from internal sources such as lights. The longwave radiation interchange includes the absorption and emittance of low temperature radiation sources, such as all other zone surfaces, equipment, and people.
The heat balance on the inside face can be written as follows:
where:
 = Net longwave radiant exchange flux between zone surfaces.
= Net longwave radiant exchange flux between zone surfaces.
 = Net short wave radiation flux to surface from lights.
= Net short wave radiation flux to surface from lights.
 = Longwave radiation flux from equipment in zone.
= Longwave radiation flux from equipment in zone.
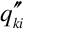 = Conduction flux through the wall.
= Conduction flux through the wall.
 = Transmitted solar radiation flux absorbed at surface.
= Transmitted solar radiation flux absorbed at surface.
 = Convective heat flux to zone air.
= Convective heat flux to zone air.
Each of these heat balance components is introduced briefly below.
Internal Long-Wave Radiation Exchange[LINK]
LW Radiation Exchange Among Zone Surfaces[LINK]
There are two limiting cases for internal LW radiation exchange that are easily modeled:
The zone air is completely transparent to LW radiation.
The zone air completely absorbs LW radiation from the surfaces within the zone.
The limiting case of completely absorbing air has been used for load calculations and also in some energy analysis calculations. This model is attractive because it can be formulated simply using a combined radiation and convection heat transfer coefficient from each surface to the zone air. However, it oversimplifies the zone surface exchange problem, and as a result, the heat balance formulation in EnergyPlus treats air as completely transparent. This means that it does not participate in the LW radiation exchange among the surfaces in the zone. The model, which considers room air to be completely transparent, is reasonable physically because of the low water vapor concentrations and the short mean path lengths. It also permits separating the radiant and convective parts of the heat transfer at the surface, which is an important attribute of the heat balance method.
EnergyPlus uses a grey interchange model for the longwave radiation among zone surfaces. This model is based on the “ScriptF” concept developed by Hottel (Hottel and Sarofim, Radiative Transfer, Chapter 3, McGraw Hill, 1967). This procedure relies on a matrix of exchange coefficients between pairs of surfaces that include all exchange paths between the surfaces. In other words all reflections, absorptions and re-emissions from other surfaces in the enclosure are included in the exchange coefficient, which is called ScriptF. The major assumptions are that all surface radiation properties are grey and all radiation is diffuse. Both assumptions are reasonable for building zone interchange.
The ScriptF coefficients are developed by starting with the traditional direct radiation view factors. In the case of building rooms and zones, there are several complicating factors in finding the direct view factors-–the main one being that the location of surfaces such as thermal mass representing furniture and partitions are not known. The other limitation is that the exact calculation of direct view factors is computationally very intensive even if the positions of all surfaces are known. Accordingly, EnergyPlus uses a procedure to approximate the direct view factors. The procedure has two steps:
- Determine the total area of other surfaces “seen” by a surface.
- Approximate the direct view factor from surface 1 to surface 2 as the ratio of the area of surface 2 to the total area “seen” by surface 1.
The determination of the “seen” area has several constraints:
- No surface sees itself.
- All surfaces see thermal mass surfaces.
- No surface facing within 10 degrees of another surface is seen by the other surface.
- All surfaces see roofs, floors and ceilings (subject to the preceding facing direction constraint).
Because the approximate view factors may not satisfy the basic requirements of reciprocity (two surfaces should exchange equal amounts of heat in each direction), and completeness (every surface should have a direct view factor sum of 1.0), EnergyPlus does a view factor fix operation before they are used in the ScriptF determination. Normally both of the requirements are satisfied, but in some special situations they are not, and special rules are applied.
- If a user includes less than four surfaces in a zone, only reciprocity is enforced.
- If the area of one surface in a zone is greater than the sum of the areas of all other surfaces, reciprocity only is enforced, but sometimes, for very large surfaces, that enforcement becomes impossible, and the view factors are modified so that only the large surface is seen by very small surfaces.
Warning messages are produced for both of these cases, and the results should be examined very carefully to ascertain that they are reasonable. The suggested action for the second case (the extra-large surface) is to divide the large surface into several smaller surfaces; then the enclosure will be treated as normal.
Once the ScriptF coefficients are determined, the longwave radiant exchange is calculated for each surface using:
where Fi,j is the ScriptF between surfaces i and j.
Thermal Mass and Furniture[LINK]
Furniture in a zone has the effect of increasing the amount of surface area that can participate in the radiation and convection heat exchanges. It also adds participating thermal mass to the zone. These two changes both affect the response to temperature changes in the zone and also affect the heat extraction characteristics.
The proper modeling of furniture is an area that needs further research, but the heat balance formulation allows the effect to be modeled in a realistic manner by including the furniture surface area and thermal mass in the heat exchange process.
LW Radiation From Internal Sources[LINK]
The traditional model for this source is to define a radiative/convective split for the heat introduced into a zone from equipment. The radiative part is then distributed over the surfaces within the zone in some prescribed manner. This, of course, is not a completely realistic model, and it departs from the heat balance principles. However, it is virtually impossible to treat this source in any more detail since the alternative would require knowledge of the placement and surface temperatures of all equipment.
Internal Short-Wave Radiation[LINK]
SW Radiation from Lights[LINK]
The short wavelength radiation from lights is distributed over the surfaces in the zone in some prescribed manner.
Transmitted Solar[LINK]
Transmitted solar radiation is also distributed over the surfaces in the zone in a prescribed manner. It would be possible to calculate the actual position of beam solar radiation, but that would involve partial surface irradiation, which is inconsistent with the rest of the zone model that assumes uniform conditions over an entire surface. The current procedures incorporate a set of prescribed distributions. Since the heat balance approach can deal with any distribution function, it is possible to change the distribution function if it seems appropriate.
Convection to Zone Air[LINK]
The convection flux is calculated using the heat transfer coefficients as follows:
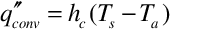 (89)
(89)
The inside convection coefficients (hc) can be calculated using one of many different models. Currently the implementation uses coefficients based on correlations for natural, mixed, and forced convection.
Interior Conduction[LINK]
This contribution to the inside surface heat balance is the wall conduction term,  shown in Equation (30). This represents the heat transfer to the inside face of the building element. Again, a CTF formulation is used to determine this heat flux.
shown in Equation (30). This represents the heat transfer to the inside face of the building element. Again, a CTF formulation is used to determine this heat flux.
Interior Convection[LINK]
There are many different modeling options available in EnergyPlus for inside convection coefficients, hc. There are four different settings to direct how EnergyPlus managers select hc models during a simulation. There are numerous individual model equations for hc in EnergyPlus to cover different situations that arise from surface orientations, room airflow conditions, and heat flow direction. Additionally, in many cases multiple researchers have developed competing models for the same situations that differ and there is no way to declare one is better than another. An overall default for the simulation is selected in the “SurfaceConvectionAlgorithm:Inside” object and can be overridden by selecting a different option in a zone description. These models are explained in the following sections. In addition to the correlation choices described below, it is also possible to override the convection coefficients on the inside of any surface by using the “SurfaceProperty:ConvectionCoefficients” object in the input file to set the convection coefficient value on the inside of any surface. The values can be specified directly or with schedules. Specific details are given in the Input Output Reference document.
Adaptive Convection Algorithm[LINK]
Beausoleil-Morrison (2000, 2002) developed a methodology for dynamically managing the selection of hc equations called adaptive convection algorithm. The algorithm is used to select among the available hc equations for the one that is most appropriate for a given surface at a given time. As Beausoleil-Morrison notes, the adaptive convection algorithm is intended to be expanded and altered to reflect different classification schemes and/or new hc equations. The implementation in EnergyPlus has been modified from the original in the following ways:
- An input mechanism is provided (see the SurfaceConvectionAlgorithm:Inside:AdapativeModelSelections object) so that the user can customize the specific selections of hc equations that are applied for different flow regimes and surface orientations. The changes apply in a general way to the entire model (but can be overridden by setting surface properties).
- To avoid requiring additional user input on the position of ZoneHVAC-type equipment within a zone, there is no distinction between zones that have convective zone heater equipment located underneath the windows and those that have convective heaters located away from the windows. This applies to the air flow regime associated with convective zone heaters. Using Beausoleil-Morrison’s terminology, regimes B1 and B2 are combined into just one B regime.
- To avoid requiring additional user input on the position of ZoneHVAC-type equipment within a zone, there is no distinction between surfaces that are directly blown on the fan and those that are away from the fan for the air flow regime associated with mechanical circulation from a zone fan (ZoneHVAC type equipment).
- The correlation for horizontal free jet developed by Fisher (1995) is not used. Ceiling diffuser models are used for all mechanical circulation from central air system. This decision was made for two reasons: (1) to avoid requiring additional user input on the position of, and momentum generated by, air terminal units, and (2) because Fisher (1995) found that the Coanda effect is so significant that in practice a free horizontal jet is difficult to maintain and mechanical-driven room airflows generally attach to surfaces and tend to match the flow regime of a ceiling diffuser much more often than a free jet.
- EnergyPlus supports arbitrary geometry so surfaces can be tilted with respect to vertical or horizontal. Beausoleil-Morrison’s adaptive convection algorithm was originally structured to use hc equations that have no functional dependence on surface tilt angle. However, tilted surfaces do perform differently than vertical or horizontal surface when buoyancy forces are significant. Therefore, the EnergyPlus implementation expands the structure of the algorithm to include additional categories for tilted surfaces. The hc equations developed by Walton (1983) are selected as the defaults for tilted surfaces because they have a functional dependence on tilt angle.
- Fohanno and Polidari (2006) produced a new hc equation for vertical walls inside buildings with a simple buoyancy flow regime. They used a theoretical approach based on integral formalism and uniform heat flux (rather than uniform temperature) that covers both laminar and turbulent flow situations. In EnergyPlus, this model is selected as the default in place of the model by Alamdari and Hammond (1983) for vertical walls.
- Karadag (2009) produced a new hc equation for ceiling surfaces that are actively chilled. He used computation fluid dynamics and various sized rooms and temperature conditions. In EnergyPlus, this model is selected as the default for surfaces that have active, in-ceiling cooling (in place of the model by Alamdari and Hammond (1983) for unstable ceilings).
- International Standard Organization (ISO) completed Standard 15099-2003 which includes hc equations for the inside face of windows. EnergyPlus strives to adhere to formal modeling Standards where possible. Therefore the implementation includes a larger structure for the adaptive algorithm that includes additional categories for windows in all flow regimes and ISO 15099-2003 models are used as the default for windows in natural convection flow regimes. The ISO 15099 model applies to various tilt angles.
- Goldstein and Novosalec (2010) produced new hc~~equations for forced air situations with ceiling slot diffusers along perimeters with significant glazing fractions. They used experiments with full-sized test room. These new equations are selected as the default for windows, ceilings and floors when there is an active central air system.
- Interior mass surfaces are assigned the hc~~equation that would apply (stable or unstable) to a horizontal, upward facing surface for each flow regime.
- The algorithm switches between forced, mixed, and natural flow regimes by calculating the Richardson number, Ri = Gr/Re^2, for the zone. Large values of Ri indicate buoyancy dominates, while small values indicate forced flows dominate. To distinguish between opposing Zone unit type equipment (with fans) are assumed to force air up walls, and central air type equipment (with diffusers) are assumed to force air down walls.
The adaptive convection algorithm implemented in EnergyPlus for the inside face has a total of 45 different categories for surfaces and 29 different options for hc equation selections. The following table summarizes the categories and the default assignments for hc equations. The individual hc equations are documented below.
Inside Convection Categories and Assignments
Zone Air Flow Regime
IB-M’s #
Surface orientation and heat flow direction
Keywords for Applicable Model Equation Sources
1
Simple Buoyancy
A3
Vertical Walls
FohannoPolidoriVerticalWall*AlamdariHammondVerticalWallASHRAEVerticalWall
2
Stable Horizontal
AlamdariHammondStableHorizontal*WaltonStableHorizontalOrTilt
3
Unstable Horizontal
AlamdariHammondUnstableHorizontal*WaltonUnstableHorizontalOrTilt
4
Stable Tilted
WaltonStableHorizontalOrTilt*
5
Unstable Tilted
WaltonUnstableHorizontalOrTilt*
6
Windows
ISO15099Windows*
7
In-floor Heating or In-ceiling Cooling
A1
Vertical Walls
KhalifaEq3WallAwayFromHeat*FohannoPolidoriVerticalWallAlamdariHammondVerticalWallASHRAEVerticalWall
8
Stable Horizontal
AlamdariHammondStableHorizontal*WaltonStableHorizontalOrTilt
9
Unstable Horizontal
KhalifaEq4CeilingAwayFromHeat*AlamdariHammondUnstableHorizontal WaltonUnstableHorizontalOrTilt
10
Heated Floor
AwbiHattonHeatedFloor*WaltonUnstableHorizontalOrTiltAlamdariHammondUnstableHorizontal
11
Chilled Ceiling
KaradagChilledCeiling*WaltonUnstableHorizontalOrTilt
12
Stable Tilted
WaltonStableHorizontalOrTilt*
13
Unstable Tilted
WaltonUnstableHorizontalOrTilt*
14
Windows
ISO15099Windows*
15
Wall Panel Heating
A2
Vertical Walls (non-heated)
KhalifaEq6NonHeatedWalls*FohannoPolidoriVerticalWallASHRAEVerticalWall
16
Heated Wall
AwbiHattonHeatedWall*
17
Stable Horizontal
AlamdariHammondStableHorizontal*WaltonStableHorizontalOrTilt
18
Unstable Horizontal
KhalifaEq7Ceiling*AlamdariHammondUnstableHorizontalWaltonUnstableHorizontalOrTilt
19
Stable Tilted
WaltonStableHorizontalOrTilt*
20
Unstable Tilted
WaltonUnstableHorizontalOrTilt*
21
Windows
ISO15099Windows*
22
Convective Zone Heater
B
Vertical Walls not near heater
FohannoPolidoriVerticalWall*KhalifaEq6NonHeatedWallsKhalifaEq3WallAwayFromHeatAlamdariHammondVerticalWallASHRAEVerticalWall
23
Vertical Walls near heater
KhalifaEq5WallNearHeat*
24
Stable Horizontal
AlamdariHammondStableHorizontal*WaltonStableHorizontalOrTilt
25
Unstable Horizontal
KhalifaEq7Ceiling*KhalifaEq4CeilingAwayFromHeatWaltonUnstableHorizontalOrTilt
26
Stable Tilted
WaltonStableHorizontalOrTilt*
27
Unstable Tilted
WaltonUnstableHorizontalOrTilt*
28
Windows
ISO15099Windows*
29
Mechanical Central Air Diffuser
C
Walls
GoldsteinNovoselacCeilingDiffuserWalls*
30
Ceiling
FisherPedersenCeilingDiffuserCeiling*
31
Floor
GoldsteinNovoselacCeilingDiffuserFloor*
32
Windows
GoldsteinNovoselacCeilingDiffuserWindow*
33
Mechanical Zone Fan Circulation
D
Walls
KhalifaEq3WallAwayFromHeat*
34
Stable Horizontal
AlamdariHammondStableHorizontal*WaltonStableHorizontalOrTilt
35
Unstable Horizontal
KhalifaEq4CeilingAwayFromHeat*WaltonUnstableHorizontalOrTilt
36
Stable Tilted
WaltonStableHorizontalOrTilt*
37
Unstable Tilted
WaltonUnstableHorizontalOrTilt*
38
Windows
GoldsteinNovoselacCeilingDiffuserWindow*
39
Mixed
E
Assisting Flow Walls
BeausoleilMorrisonMixedAssistedWall*
40
Opposing Flow Walls
BeausoleilMorrisonMixedOpposingWall*
41
Stable Floor
BeausoleilMorrisonMixedStableFloor*
42
Unstable Floor
BeausoleilMorrisonMixedUnstableFloor*
43
Stable Ceiling
BeausoleilMorrisonMixedStableCeiling*
44
Unstable Ceiling
BeausoleilMorrisonMixedUnstableCeiling*
45
Windows
GoldsteinNovoselacCeilingDiffuserWindow*
* Indicates the default selection for hc model equation.
Inside Face Surface Classification[LINK]
The adaptive convection algorithm is based on classifying surfaces by flow regime and orientation so that the correct hc equation can be chosen at a particular point in time during the simulation. The classification depends on user input with some aspects processed only once at the beginning and others during each timestep. There are also various parameters or inputs to the hc equations that need static or dynamic processing.
For each surface, it and the zone it is attached to are processed for the following static characteristics.
- Characteristic height for convection is taken as the zone height.
- Surfaces listed as receiving heat from Zone HVAC equipment with radiative models are considered “near” the heater.
- Zones are examined for low temperature radiant systems. The surfaces that contain the active elements are examined and the zone characterized to know if it has in-floor heating, in-ceiling cooling, or in-wall heating.
- A hydraulic diameter is calculated for horizontal surfaces for the entire zone.
and calculating various parameters needed by hc equations. Selecting flow regime is done in the following manner. For each surface, we examine the zone on the inside face for the following:
- HVAC system type
- HVAC operating status
- HVAC system ACH
The surfaces are evaluated to determine:
- Surface classification: Floor, wall, roof, window, types
- Tilt angle
- Convective stability (sign of ΔT)
The individual hc model equations and their respective references are listed in next by the keyword used to identify them.
ASHRAE Vertical Wall[LINK]
Walton adopted the following equation for natural convection from ASHRAE .
This is usually bound at a minimum of .1 in EnergyPlus. This is a component of the TARP overall algorithm described below.
Walton Unstable Horizontal Or Tilt[LINK]
Walton (11983) developed the following equation by fitting curves from various sources.
Unstable refers to the direction of heat flow and the associated buoyancy relative to the surfaces. Unstable is when the natural tendency is to enhance flow in the sense that rising warmer air, or falling cooler air, is free to move away from the surface. This is usually bound at a minimum of .1 in EnergyPlus. This is a component of the TARP overall algorithm described below.
Walton Stable Horizontal Or Tilt[LINK]
Walton (11983) developed the following equation by fitting curves from various sources.
Stable refers to the direction of heat flow and the associated buoyancy relative to the surfaces. Stable is when the natural tendency is to retard flow in the sense that rising warmer air, or falling cooler air, is driven against the surface. This is usually bound at a minimum of .1 in EnergyPlus. This is a component of the TARP overall algorithm described below.
Fisher Pedersen Ceiling Diffuser Walls[LINK]
Fisher and Pedersen 1997) developed the following equation from laboratory chamber measurements.
This is a component of the CeilingDiffuser overall algorithm described below.
Fisher Pedersen Ceiling Diffuser Ceiling[LINK]
Fisher and Pedersen 1997) developed the following equation from laboratory chamber measurements.
This is a component of the CeilingDiffuser overall algorithm described below.
Fisher Pedersen Ceiling Diffuser Floor[LINK]
Fisher and Pedersen 1997) developed the following equation from laboratory chamber measurements.
This is a component of the CeilingDiffuser overall algorithm described below.
Alamdari Hammond Stable Horizontal[LINK]
Alamdari and Hammond (1983) developed the following correlation for horizontal surfaces in stable thermal situation.
where,
 , hydraulic diameter of horizontal surface, A is area (m2) and P is the perimeter (m) of the entire zone.
, hydraulic diameter of horizontal surface, A is area (m2) and P is the perimeter (m) of the entire zone.
Alamdari Hammond Unstable Horizontal[LINK]
Alamdari and Hammond (1983) developed the following correlation for horizontal surfaces in a buoyant thermal situation.
Alamdari Hammond Vertical Wall[LINK]
Alamdari and Hammond (1983) developed the following correlation for vertical surfaces.
where,
H is the characteristic height for the surface. In EnergyPlus this is the zone’s ceiling height (which could be larger than the height of an individual surface when wall are subdivided into more than one surface).
Khalifa Eq3 Wall Away From Heat[LINK]
Khalifa (1989) conducted experiments with test chambers and developed correlations for certain types of surfaces. One of them, identified as “Equation 3” in original reference, is for convectively heated zones and applies to the inside surfaces of walls away from the heat source:
Khalifa Eq4 Ceiling Away From Heat[LINK]
Khalifa (1989) conducted experiments with test chambers and developed correlations for certain types of surfaces. One of them, identified as “Equation 4” in original reference, is for convectively heated zones and applies to the inside surfaces of ceilings away from the heat source:
Khalifa Eq5 Wall Near Heat[LINK]
Khalifa (1989) conducted experiments with test chambers and developed correlations for certain types of surfaces. One of them, identified as “Equation 5” in original reference, is for convectively heated zones and applies to the inside surfaces of walls near the heat source:
Khalifa Eq6 Non Heated Walls[LINK]
Khalifa (1989) conducted experiments with test chambers and developed correlations for certain types of surfaces. One of them, identified as “Equation 6” in original reference, is for heated zones and applies to the inside surfaces of walls that are not heated:
Khalifa Eq7 Ceiling[LINK]
Khalifa (1989) conducted experiments with test chambers and developed correlations for certain types of surfaces. One of them, identified as “Equation 7” in original reference, is for heated zones and applies to the inside surfaces of ceilings:
Awbi Hatton Heated Floor[LINK]
Awbi and Hatton (1999) conducted laboratory measurements using environmental chambers and developed the following correlation for floor surfaces that are being actively heated.
where,
 , hydraulic diameter of horizontal surface, A is area (m2) and P is the perimeter (m) of the entire zone (all of the adjacent floor surfaces if more than one in the zone).
, hydraulic diameter of horizontal surface, A is area (m2) and P is the perimeter (m) of the entire zone (all of the adjacent floor surfaces if more than one in the zone).
Awbi Hatton Heated Wall[LINK]
Awbi and Hatton (1999) developed the following correlation for wall surfaces that are being actively heated.
where,
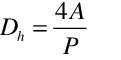 , hydraulic diameter of wall surface, A is area (m2) and P is the perimeter (m) of the entire wall (all of the adjacent wall surfaces if more than one along the wall).
, hydraulic diameter of wall surface, A is area (m2) and P is the perimeter (m) of the entire wall (all of the adjacent wall surfaces if more than one along the wall).
Beausoleil Morrison Mixed Assisted Wall[LINK]
Beausoleil-Morrison (2000) used blending techniques to combine correlations originally developed by Alamdari and Hammond (1983) and Fisher and Pedersen (1997) to create the following correlation is for walls where the flow driving forces from mechanical forces are augmented by the driving forces from buoyancy.
where,
TSAT~~is the supply air temperature at the diffuser.
Here the reference temperature is the zone air temperature rather than the diffuser supply air temperature.
Beausoleil Morrison Mixed Opposing Wall[LINK]
Beausoleil-Morrison (2000) used blending techniques to combine correlations originally developed by Alamdari and Hammond (1983) and Fisher and Pedersen (1997) to create the following correlation is for walls where the flow driving forces from mechanical forces are opposed by the driving forces from buoyancy.
Beausoleil Morrison Mixed Stable Floor[LINK]
Beausoleil-Morrison (2000) used blending techniques to combine correlations originally developed by Alamdari and Hammond (1983) and Fisher and Pedersen (1997) to create the following correlation is for floors where the flow driving forces include both mechanical forces and thermally stable buoyancy.
Beausoleil Morrison Mixed Unstable Floor[LINK]
Beausoleil-Morrison (2000) used blending techniques to combine correlations originally developed by Alamdari and Hammond (1983) and Fisher and Pedersen (1997) to create the following correlation is for floors where the flow driving forces include both mechanical forces and thermally unstable buoyancy.
Beausoleil Morrison Mixed Stable Ceiling[LINK]
Beausoleil-Morrison (2000) used blending techniques to combine correlations originally developed by Alamdari and Hammond (1983) and Fisher and Pedersen (1997) to create the following correlation is for ceilings where the flow driving forces include both mechanical forces and thermally Stable buoyancy.
Beausoleil Morrison Mixed Unstable Ceiling[LINK]
Beausoleil-Morrison (2000) used blending techniques to combine correlations originally developed by Alamdari and Hammond (1983) and Fisher and Pedersen (1997) to create the following correlation is for ceilings where the flow driving forces include both mechanical forces and thermally unstable buoyancy.
Karadag Chilled Ceiling[LINK]
Karadag (2009) used numerical methods to develop the following equation for hc for chilled-ceiling surfaces.
ISO 15099 Windows[LINK]
ISO Standard 15099-2003 includes the equations for hc for room-side of windows and surfaces with any tilt angle and heat flow direction. The ISO 15099 correlation is for still room air angle and is determined in terms of the Nusselt number,  , where
, where
where,
 is the thermal conductivity of air, and
is the thermal conductivity of air, and
 is the height of the window.
is the height of the window.
The Rayleigh number based on height, 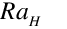 , is calculated using,
, is calculated using,
where,
 is the density of air
is the density of air
 is the acceleration due to gravity,
is the acceleration due to gravity,
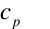 is the specific heat of air,
is the specific heat of air,
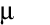 is the dynamic viscosity of air, and
is the dynamic viscosity of air, and
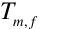 is the mean film temperature in Kelvin given by,
is the mean film temperature in Kelvin given by,
There are four cases for the Nusselt correlation that vary by the tilt angle in degrees,  , and are based on heating conditions. For cooling conditions (where
, and are based on heating conditions. For cooling conditions (where  ) the tilt angle is complemented so that
) the tilt angle is complemented so that 
Case A. 
Case B. 
Case C. 
Case D. 
The material properties are evaluated at the mean film temperature. Standard EnergyPlus psychrometric functions are used for  and
and 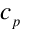 . Thermal conductivity is calculated using,
. Thermal conductivity is calculated using,
 .
.
Kinematic viscosity is calculated using,
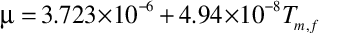 .
.
This correlation depends on the surface temperature of the room-side glazing surface and is therefore included inside the window heat balance iteration loop.
Goldstein Novoselac Ceiling Diffuser Window[LINK]
Goldstein and Novoselac (2010) used laboratory chamber measurements to develop convection correlations for perimeter zones with highly glazed spaces served by overhead slot-diffuser-based air systems. The following are for bare windows in such spaces.
For WWR<50% with window in upper part of wall:
For WWR<50% with window in lower part of wall
For WWR > 50%
Where,
WWR is the window to wall ratio.
L is the length of exterior wall with glazing in the zone.
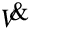 is the air system flow rate in m3/s.
is the air system flow rate in m3/s.
Goldstein Novoselac Ceiling Diffuser Walls[LINK]
Goldstein and Novoselac (2010) used laboratory chamber measurements to develop convection correlations for perimeter zones with highly glazed spaces served by overhead slot-diffuser-based air systems. The following are for exterior walls in such spaces.
For walls located below a window
For walls located above a window
Goldstein Novoselac Ceiling Diffuser Floor[LINK]
Goldstein and Novoselac (2010) used laboratory chamber measurements to develop convection correlations for perimeter zones with highly glazed spaces served by overhead slot-diffuser-based air systems. The following is for floors in such spaces.
Separate from the above model structure, there are also other comprehensive algorithm structures which are described below.
TARP Algorithm[LINK]
The comprehensive natural convection model, accessed using the keyword “TARP,” correlates the convective heat transfer coefficient to the surface orientation and the difference between the surface and zone air temperatures (where T = Surface Temperature - Air Temperature). The algorithm is taken directly from Walton (1983). Walton derived his algorithm from ASHRAE literature which can now be found for example in the ASHRAE Handbook (HoF 2001), Table 5 on p. 3.12, which gives equations for natural convection heat transfer coefficients in the turbulent range for large, vertical plates and for large, horizontal plates facing upward when heated (or downward when cooled). A note in the text also gives an approximation for large, horizontal plates facing downward when heated (or upward when cooled) recommending that it should be half of the facing upward value. Walton adds a curve fit as a function of the cosine of the tilt angle to provide intermediate values between vertical and horizontal. The curve fit values at the extremes match the ASHRAE values very well.
For no temperature difference OR a vertical surface the following correlation is used:
 (90)
(90)
For (T < 0.0 AND an upward facing surface) OR (T > 0.0 AND an downward facing surface) an enhanced convection correlation is used:
 (91)
(91)
where is the surface tilt angle.
For (T > 0.0 AND an upward facing surface) OR (T < 0.0 AND an downward facing surface) a reduced convection correlation is used:
 (92)
(92)
where is the surface tilt angle.
Simple Natural Convection Algorithm[LINK]
The simple convection model uses constant coefficients for different heat transfer configurations, using the same criteria as the detailed model to determine reduced and enhanced convection. The coefficients are also taken directly from Walton (1983). Walton derived his coefficients from the surface conductances for =0.90 found in the ASHRAE Handbook (1985) in Table 1 on p. 23.2. The radiative heat transfer component was estimated at 1.02 * 0.9 = 0.918 BTU/h-ft2-F and then subtracted off. Finally the coefficients were converted to SI units to yield the values below.
For a vertical surface:
For a horizontal surface with reduced convection:
For a horizontal surface with enhanced convection:
For a tilted surface with reduced convection:
For a tilted surface with enhanced convection:
Ceiling Diffuser Algorithm[LINK]
The ceiling diffuser algorithm is based on empirical correlations developed by Fisher and Pedersen (1997). The correlation was reformulated to use the room outlet temperature as the reference temperature. The correlations are shown below.
For Floors:
 (93)
(93)
The correlation for floors is illustrated in the following figure:
For ceilings:
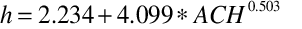 (94)
(94)
The correlation for ceilings is illustrated in the following figure:
For Walls:
 (95)
(95)
The correlation for walls is illustrated in the following figure:
Trombe Wall Algorithm[LINK]
The Trombe wall algorithm is used to model convection in a “Trombe wall zone”, i.e. the air space between the storage wall surface and the exterior glazing. (See the later sections on Passive and Active Trombe Walls below for more information about Trombe walls.) The algorithm is identical to the convection model (based on ISO 15099) used in Window5 for convection between glazing layers in multi-pane window systems. The use of the algorithm for modeling an unvented Trombe wall has been validated against experimental data by Ellis (2003).
This algorithm gives the convection coefficients for air in a narrow vertical cavity that is sealed and not ventilated. This applies both to the air gap in between panes of a window or to the air gap between the Trombe wall glazing and the inner surface (often a selective surface). These convection coefficients are really the only difference between a normal zone and a Trombe zone. The rest of the zone heat balance is the same, e.g., transmitted solar, long-wave radiation between surfaces, etc.
For a vertical cavity, the correlation from ISO 15099 is:
 for 5E4 < Ra < 1E6
for 5E4 < Ra < 1E6
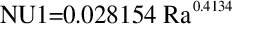 for 1E4 < Ra < 5E4
for 1E4 < Ra < 5E4
 for Ra <= 1E4
for Ra <= 1E4
where
Nu = Nusselt number
Ra = Rayleigh number
A = aspect ratio of cavity
This is then used in EnergyPlus as follows:
Net convection coefficient from glazing to wall is:
where
k = conductivity of air
L = air gap thickness
Convection coefficient applied to each wall separately and actually used in the zone heat balance is:
Alamdari, F. and G.P. Hammond. 1983. Improved data correlations for buoyancy-driven convection in rooms. Building Services Engineering Research & Technology. Vol. 4, No. 3.
ASHRAE. 1985. 1985 ASHRAE Handbook – Fundamentals, Atlanta: American Society of Heating, Refrigerating, and Air-Conditioning Engineers, Inc.
ASHRAE. 2001. 2001 ASHRAE Handbook – Fundamentals, Atlanta: American Society of Heating, Refrigerating, and Air-Conditioning Engineers, Inc.
Awbi, H.B. and A. Hatton. 1999. Natural convection from heated room surfaces. Energy and Buildings 30 (1999) 233-244.
Beausoleil-Morrison, I. 2000. The adaptive coupling of heat and air flow modeling within dynamic whole-building simulations. PhD. Thesis. University of Strathclyde, Glasgow, UK.
Ellis, Peter G. 2003. Development and Validation of the Unvented Trombe Wall Model in EnergyPlus. Master’s Thesis, University of Illinois at Urbana-Champaign.
Fisher, D.E. and C.O. Pedersen. 1997. “Convective Heat Transfer in Building Energy and Thermal Load Calculations”, ASHRAE Transactions, Vol. 103, Pt. 2.
Fohanno, S., and G. Polidori. 2006. Modelling of natural convective heat transfer at an internal surface. Energy and Buildings 38 (2006) 548 - 553
Goldstein, K. and A. Novoselac. 2010. Convective Heat Transfer in Rooms With Ceiling Slot Diffusers (RP-1416). HVAC&R Research Journal TBD
Karadag, R. 2009. New approach relevant to total heat transfer coefficient including the effect of radiation and convection at the ceiling in a cooled ceiling room. Applied Thermal Engineering 29 (2009) 1561-1565
Khalifa AJN. 1989. Heat transfer processes in buildings. Ph.D. Thesis, University of Wales College of Cardiff, Cardiff, UK.
ISO. 2003. ISO 15099:2003. Thermal performance of windows, doors, and shading devices – Detailed calculations. International Organization for Standardization.
Walton, G. N. 1983. Thermal Analysis Research Program Reference Manual. NBSSIR 83-2655. National Bureau of Standards (now NIST). This is documentation for “TARP.”
Inside Heat Balance[LINK]
The heart of the heat balance method is the internal heat balance involving the inside faces of the zone surfaces. This heat balance is generally modeled with four coupled heat transfer components: 1) conduction through the building element, 2) convection to the air, 3) short wave radiation absorption and reflectance and 4) longwave radiant interchange. The incident short wave radiation is from the solar radiation entering the zone through windows and emittance from internal sources such as lights. The longwave radiation interchange includes the absorption and emittance of low temperature radiation sources, such as all other zone surfaces, equipment, and people.
The heat balance on the inside face can be written as follows:
where:
Each of these heat balance components is introduced briefly below.
Internal Long-Wave Radiation Exchange[LINK]
LW Radiation Exchange Among Zone Surfaces[LINK]
There are two limiting cases for internal LW radiation exchange that are easily modeled:
The zone air is completely transparent to LW radiation.
The zone air completely absorbs LW radiation from the surfaces within the zone.
The limiting case of completely absorbing air has been used for load calculations and also in some energy analysis calculations. This model is attractive because it can be formulated simply using a combined radiation and convection heat transfer coefficient from each surface to the zone air. However, it oversimplifies the zone surface exchange problem, and as a result, the heat balance formulation in EnergyPlus treats air as completely transparent. This means that it does not participate in the LW radiation exchange among the surfaces in the zone. The model, which considers room air to be completely transparent, is reasonable physically because of the low water vapor concentrations and the short mean path lengths. It also permits separating the radiant and convective parts of the heat transfer at the surface, which is an important attribute of the heat balance method.
EnergyPlus uses a grey interchange model for the longwave radiation among zone surfaces. This model is based on the “ScriptF” concept developed by Hottel (Hottel and Sarofim, Radiative Transfer, Chapter 3, McGraw Hill, 1967). This procedure relies on a matrix of exchange coefficients between pairs of surfaces that include all exchange paths between the surfaces. In other words all reflections, absorptions and re-emissions from other surfaces in the enclosure are included in the exchange coefficient, which is called ScriptF. The major assumptions are that all surface radiation properties are grey and all radiation is diffuse. Both assumptions are reasonable for building zone interchange.
The ScriptF coefficients are developed by starting with the traditional direct radiation view factors. In the case of building rooms and zones, there are several complicating factors in finding the direct view factors-–the main one being that the location of surfaces such as thermal mass representing furniture and partitions are not known. The other limitation is that the exact calculation of direct view factors is computationally very intensive even if the positions of all surfaces are known. Accordingly, EnergyPlus uses a procedure to approximate the direct view factors. The procedure has two steps:
The determination of the “seen” area has several constraints:
Because the approximate view factors may not satisfy the basic requirements of reciprocity (two surfaces should exchange equal amounts of heat in each direction), and completeness (every surface should have a direct view factor sum of 1.0), EnergyPlus does a view factor fix operation before they are used in the ScriptF determination. Normally both of the requirements are satisfied, but in some special situations they are not, and special rules are applied.
Warning messages are produced for both of these cases, and the results should be examined very carefully to ascertain that they are reasonable. The suggested action for the second case (the extra-large surface) is to divide the large surface into several smaller surfaces; then the enclosure will be treated as normal.
Once the ScriptF coefficients are determined, the longwave radiant exchange is calculated for each surface using:
where Fi,j is the ScriptF between surfaces i and j.
Thermal Mass and Furniture[LINK]
Furniture in a zone has the effect of increasing the amount of surface area that can participate in the radiation and convection heat exchanges. It also adds participating thermal mass to the zone. These two changes both affect the response to temperature changes in the zone and also affect the heat extraction characteristics.
The proper modeling of furniture is an area that needs further research, but the heat balance formulation allows the effect to be modeled in a realistic manner by including the furniture surface area and thermal mass in the heat exchange process.
LW Radiation From Internal Sources[LINK]
The traditional model for this source is to define a radiative/convective split for the heat introduced into a zone from equipment. The radiative part is then distributed over the surfaces within the zone in some prescribed manner. This, of course, is not a completely realistic model, and it departs from the heat balance principles. However, it is virtually impossible to treat this source in any more detail since the alternative would require knowledge of the placement and surface temperatures of all equipment.
Internal Short-Wave Radiation[LINK]
SW Radiation from Lights[LINK]
The short wavelength radiation from lights is distributed over the surfaces in the zone in some prescribed manner.
Transmitted Solar[LINK]
Transmitted solar radiation is also distributed over the surfaces in the zone in a prescribed manner. It would be possible to calculate the actual position of beam solar radiation, but that would involve partial surface irradiation, which is inconsistent with the rest of the zone model that assumes uniform conditions over an entire surface. The current procedures incorporate a set of prescribed distributions. Since the heat balance approach can deal with any distribution function, it is possible to change the distribution function if it seems appropriate.
Convection to Zone Air[LINK]
The convection flux is calculated using the heat transfer coefficients as follows:
The inside convection coefficients (hc) can be calculated using one of many different models. Currently the implementation uses coefficients based on correlations for natural, mixed, and forced convection.
Interior Conduction[LINK]
This contribution to the inside surface heat balance is the wall conduction term, shown in Equation (30). This represents the heat transfer to the inside face of the building element. Again, a CTF formulation is used to determine this heat flux.
shown in Equation (30). This represents the heat transfer to the inside face of the building element. Again, a CTF formulation is used to determine this heat flux.
Interior Convection[LINK]
There are many different modeling options available in EnergyPlus for inside convection coefficients, hc. There are four different settings to direct how EnergyPlus managers select hc models during a simulation. There are numerous individual model equations for hc in EnergyPlus to cover different situations that arise from surface orientations, room airflow conditions, and heat flow direction. Additionally, in many cases multiple researchers have developed competing models for the same situations that differ and there is no way to declare one is better than another. An overall default for the simulation is selected in the “SurfaceConvectionAlgorithm:Inside” object and can be overridden by selecting a different option in a zone description. These models are explained in the following sections. In addition to the correlation choices described below, it is also possible to override the convection coefficients on the inside of any surface by using the “SurfaceProperty:ConvectionCoefficients” object in the input file to set the convection coefficient value on the inside of any surface. The values can be specified directly or with schedules. Specific details are given in the Input Output Reference document.
Adaptive Convection Algorithm[LINK]
Beausoleil-Morrison (2000, 2002) developed a methodology for dynamically managing the selection of hc equations called adaptive convection algorithm. The algorithm is used to select among the available hc equations for the one that is most appropriate for a given surface at a given time. As Beausoleil-Morrison notes, the adaptive convection algorithm is intended to be expanded and altered to reflect different classification schemes and/or new hc equations. The implementation in EnergyPlus has been modified from the original in the following ways:
The adaptive convection algorithm implemented in EnergyPlus for the inside face has a total of 45 different categories for surfaces and 29 different options for hc equation selections. The following table summarizes the categories and the default assignments for hc equations. The individual hc equations are documented below.
Inside Convection Categories and Assignments
Zone Air Flow Regime
IB-M’s #
Surface orientation and heat flow direction
Keywords for Applicable Model Equation Sources
1
Simple Buoyancy
A3
Vertical Walls
FohannoPolidoriVerticalWall*AlamdariHammondVerticalWallASHRAEVerticalWall
2
Stable Horizontal
AlamdariHammondStableHorizontal*WaltonStableHorizontalOrTilt
3
Unstable Horizontal
AlamdariHammondUnstableHorizontal*WaltonUnstableHorizontalOrTilt
4
Stable Tilted
WaltonStableHorizontalOrTilt*
5
Unstable Tilted
WaltonUnstableHorizontalOrTilt*
6
Windows
ISO15099Windows*
7
In-floor Heating or In-ceiling Cooling
A1
Vertical Walls
KhalifaEq3WallAwayFromHeat*FohannoPolidoriVerticalWallAlamdariHammondVerticalWallASHRAEVerticalWall
8
Stable Horizontal
AlamdariHammondStableHorizontal*WaltonStableHorizontalOrTilt
9
Unstable Horizontal
KhalifaEq4CeilingAwayFromHeat*AlamdariHammondUnstableHorizontal WaltonUnstableHorizontalOrTilt
10
Heated Floor
AwbiHattonHeatedFloor*WaltonUnstableHorizontalOrTiltAlamdariHammondUnstableHorizontal
11
Chilled Ceiling
KaradagChilledCeiling*WaltonUnstableHorizontalOrTilt
12
Stable Tilted
WaltonStableHorizontalOrTilt*
13
Unstable Tilted
WaltonUnstableHorizontalOrTilt*
14
Windows
ISO15099Windows*
15
Wall Panel Heating
A2
Vertical Walls (non-heated)
KhalifaEq6NonHeatedWalls*FohannoPolidoriVerticalWallASHRAEVerticalWall
16
Heated Wall
AwbiHattonHeatedWall*
17
Stable Horizontal
AlamdariHammondStableHorizontal*WaltonStableHorizontalOrTilt
18
Unstable Horizontal
KhalifaEq7Ceiling*AlamdariHammondUnstableHorizontalWaltonUnstableHorizontalOrTilt
19
Stable Tilted
WaltonStableHorizontalOrTilt*
20
Unstable Tilted
WaltonUnstableHorizontalOrTilt*
21
Windows
ISO15099Windows*
22
Convective Zone Heater
B
Vertical Walls not near heater
FohannoPolidoriVerticalWall*KhalifaEq6NonHeatedWallsKhalifaEq3WallAwayFromHeatAlamdariHammondVerticalWallASHRAEVerticalWall
23
Vertical Walls near heater
KhalifaEq5WallNearHeat*
24
Stable Horizontal
AlamdariHammondStableHorizontal*WaltonStableHorizontalOrTilt
25
Unstable Horizontal
KhalifaEq7Ceiling*KhalifaEq4CeilingAwayFromHeatWaltonUnstableHorizontalOrTilt
26
Stable Tilted
WaltonStableHorizontalOrTilt*
27
Unstable Tilted
WaltonUnstableHorizontalOrTilt*
28
Windows
ISO15099Windows*
29
Mechanical Central Air Diffuser
C
Walls
GoldsteinNovoselacCeilingDiffuserWalls*
30
Ceiling
FisherPedersenCeilingDiffuserCeiling*
31
Floor
GoldsteinNovoselacCeilingDiffuserFloor*
32
Windows
GoldsteinNovoselacCeilingDiffuserWindow*
33
Mechanical Zone Fan Circulation
D
Walls
KhalifaEq3WallAwayFromHeat*
34
Stable Horizontal
AlamdariHammondStableHorizontal*WaltonStableHorizontalOrTilt
35
Unstable Horizontal
KhalifaEq4CeilingAwayFromHeat*WaltonUnstableHorizontalOrTilt
36
Stable Tilted
WaltonStableHorizontalOrTilt*
37
Unstable Tilted
WaltonUnstableHorizontalOrTilt*
38
Windows
GoldsteinNovoselacCeilingDiffuserWindow*
39
Mixed
E
Assisting Flow Walls
BeausoleilMorrisonMixedAssistedWall*
40
Opposing Flow Walls
BeausoleilMorrisonMixedOpposingWall*
41
Stable Floor
BeausoleilMorrisonMixedStableFloor*
42
Unstable Floor
BeausoleilMorrisonMixedUnstableFloor*
43
Stable Ceiling
BeausoleilMorrisonMixedStableCeiling*
44
Unstable Ceiling
BeausoleilMorrisonMixedUnstableCeiling*
45
Windows
GoldsteinNovoselacCeilingDiffuserWindow*
* Indicates the default selection for hc model equation.
Inside Face Surface Classification[LINK]
The adaptive convection algorithm is based on classifying surfaces by flow regime and orientation so that the correct hc equation can be chosen at a particular point in time during the simulation. The classification depends on user input with some aspects processed only once at the beginning and others during each timestep. There are also various parameters or inputs to the hc equations that need static or dynamic processing.
For each surface, it and the zone it is attached to are processed for the following static characteristics.
and calculating various parameters needed by hc equations. Selecting flow regime is done in the following manner. For each surface, we examine the zone on the inside face for the following:
The surfaces are evaluated to determine:
The individual hc model equations and their respective references are listed in next by the keyword used to identify them.
ASHRAE Vertical Wall[LINK]
Walton adopted the following equation for natural convection from ASHRAE .
This is usually bound at a minimum of .1 in EnergyPlus. This is a component of the TARP overall algorithm described below.
Walton Unstable Horizontal Or Tilt[LINK]
Walton (11983) developed the following equation by fitting curves from various sources.
Unstable refers to the direction of heat flow and the associated buoyancy relative to the surfaces. Unstable is when the natural tendency is to enhance flow in the sense that rising warmer air, or falling cooler air, is free to move away from the surface. This is usually bound at a minimum of .1 in EnergyPlus. This is a component of the TARP overall algorithm described below.
Walton Stable Horizontal Or Tilt[LINK]
Walton (11983) developed the following equation by fitting curves from various sources.
Stable refers to the direction of heat flow and the associated buoyancy relative to the surfaces. Stable is when the natural tendency is to retard flow in the sense that rising warmer air, or falling cooler air, is driven against the surface. This is usually bound at a minimum of .1 in EnergyPlus. This is a component of the TARP overall algorithm described below.
Fisher Pedersen Ceiling Diffuser Walls[LINK]
Fisher and Pedersen 1997) developed the following equation from laboratory chamber measurements.
This is a component of the CeilingDiffuser overall algorithm described below.
Fisher Pedersen Ceiling Diffuser Ceiling[LINK]
Fisher and Pedersen 1997) developed the following equation from laboratory chamber measurements.
This is a component of the CeilingDiffuser overall algorithm described below.
Fisher Pedersen Ceiling Diffuser Floor[LINK]
Fisher and Pedersen 1997) developed the following equation from laboratory chamber measurements.
This is a component of the CeilingDiffuser overall algorithm described below.
Alamdari Hammond Stable Horizontal[LINK]
Alamdari and Hammond (1983) developed the following correlation for horizontal surfaces in stable thermal situation.
where,
Alamdari Hammond Unstable Horizontal[LINK]
Alamdari and Hammond (1983) developed the following correlation for horizontal surfaces in a buoyant thermal situation.
Alamdari Hammond Vertical Wall[LINK]
Alamdari and Hammond (1983) developed the following correlation for vertical surfaces.
where,
H is the characteristic height for the surface. In EnergyPlus this is the zone’s ceiling height (which could be larger than the height of an individual surface when wall are subdivided into more than one surface).
Khalifa Eq3 Wall Away From Heat[LINK]
Khalifa (1989) conducted experiments with test chambers and developed correlations for certain types of surfaces. One of them, identified as “Equation 3” in original reference, is for convectively heated zones and applies to the inside surfaces of walls away from the heat source:
Khalifa Eq4 Ceiling Away From Heat[LINK]
Khalifa (1989) conducted experiments with test chambers and developed correlations for certain types of surfaces. One of them, identified as “Equation 4” in original reference, is for convectively heated zones and applies to the inside surfaces of ceilings away from the heat source:
Khalifa Eq5 Wall Near Heat[LINK]
Khalifa (1989) conducted experiments with test chambers and developed correlations for certain types of surfaces. One of them, identified as “Equation 5” in original reference, is for convectively heated zones and applies to the inside surfaces of walls near the heat source:
Khalifa Eq6 Non Heated Walls[LINK]
Khalifa (1989) conducted experiments with test chambers and developed correlations for certain types of surfaces. One of them, identified as “Equation 6” in original reference, is for heated zones and applies to the inside surfaces of walls that are not heated:
Khalifa Eq7 Ceiling[LINK]
Khalifa (1989) conducted experiments with test chambers and developed correlations for certain types of surfaces. One of them, identified as “Equation 7” in original reference, is for heated zones and applies to the inside surfaces of ceilings:
Awbi Hatton Heated Floor[LINK]
Awbi and Hatton (1999) conducted laboratory measurements using environmental chambers and developed the following correlation for floor surfaces that are being actively heated.
where,
Awbi Hatton Heated Wall[LINK]
Awbi and Hatton (1999) developed the following correlation for wall surfaces that are being actively heated.
where,
Beausoleil Morrison Mixed Assisted Wall[LINK]
Beausoleil-Morrison (2000) used blending techniques to combine correlations originally developed by Alamdari and Hammond (1983) and Fisher and Pedersen (1997) to create the following correlation is for walls where the flow driving forces from mechanical forces are augmented by the driving forces from buoyancy.
where,
TSAT~~is the supply air temperature at the diffuser.
Here the reference temperature is the zone air temperature rather than the diffuser supply air temperature.
Beausoleil Morrison Mixed Opposing Wall[LINK]
Beausoleil-Morrison (2000) used blending techniques to combine correlations originally developed by Alamdari and Hammond (1983) and Fisher and Pedersen (1997) to create the following correlation is for walls where the flow driving forces from mechanical forces are opposed by the driving forces from buoyancy.
Beausoleil Morrison Mixed Stable Floor[LINK]
Beausoleil-Morrison (2000) used blending techniques to combine correlations originally developed by Alamdari and Hammond (1983) and Fisher and Pedersen (1997) to create the following correlation is for floors where the flow driving forces include both mechanical forces and thermally stable buoyancy.
Beausoleil Morrison Mixed Unstable Floor[LINK]
Beausoleil-Morrison (2000) used blending techniques to combine correlations originally developed by Alamdari and Hammond (1983) and Fisher and Pedersen (1997) to create the following correlation is for floors where the flow driving forces include both mechanical forces and thermally unstable buoyancy.
Beausoleil Morrison Mixed Stable Ceiling[LINK]
Beausoleil-Morrison (2000) used blending techniques to combine correlations originally developed by Alamdari and Hammond (1983) and Fisher and Pedersen (1997) to create the following correlation is for ceilings where the flow driving forces include both mechanical forces and thermally Stable buoyancy.
Beausoleil Morrison Mixed Unstable Ceiling[LINK]
Beausoleil-Morrison (2000) used blending techniques to combine correlations originally developed by Alamdari and Hammond (1983) and Fisher and Pedersen (1997) to create the following correlation is for ceilings where the flow driving forces include both mechanical forces and thermally unstable buoyancy.
!!! {:error “Image in Header” :alt “” :img “media/image316.png”} !!! Fohanno Polidori Vertical Wall[LINK]
Fohanno and Polidori (2006) developed the following equation for hc for vertical walls under simple buoyancy flow conditions.
where,
Karadag Chilled Ceiling[LINK]
Karadag (2009) used numerical methods to develop the following equation for hc for chilled-ceiling surfaces.
ISO 15099 Windows[LINK]
ISO Standard 15099-2003 includes the equations for hc for room-side of windows and surfaces with any tilt angle and heat flow direction. The ISO 15099 correlation is for still room air angle and is determined in terms of the Nusselt number, , where
, where
where,
The Rayleigh number based on height,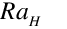 , is calculated using,
, is calculated using,
where,
There are four cases for the Nusselt correlation that vary by the tilt angle in degrees, , and are based on heating conditions. For cooling conditions (where
, and are based on heating conditions. For cooling conditions (where  ) the tilt angle is complemented so that
) the tilt angle is complemented so that 
Case A.
Case B.
Case C.
Case D.
The material properties are evaluated at the mean film temperature. Standard EnergyPlus psychrometric functions are used for and
and 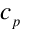 . Thermal conductivity is calculated using,
. Thermal conductivity is calculated using,
Kinematic viscosity is calculated using,
This correlation depends on the surface temperature of the room-side glazing surface and is therefore included inside the window heat balance iteration loop.
Goldstein Novoselac Ceiling Diffuser Window[LINK]
Goldstein and Novoselac (2010) used laboratory chamber measurements to develop convection correlations for perimeter zones with highly glazed spaces served by overhead slot-diffuser-based air systems. The following are for bare windows in such spaces.
For WWR<50% with window in upper part of wall:
For WWR<50% with window in lower part of wall
For WWR > 50%
Where,
WWR is the window to wall ratio.
L is the length of exterior wall with glazing in the zone.
Goldstein Novoselac Ceiling Diffuser Walls[LINK]
Goldstein and Novoselac (2010) used laboratory chamber measurements to develop convection correlations for perimeter zones with highly glazed spaces served by overhead slot-diffuser-based air systems. The following are for exterior walls in such spaces.
For walls located below a window
For walls located above a window
Goldstein Novoselac Ceiling Diffuser Floor[LINK]
Goldstein and Novoselac (2010) used laboratory chamber measurements to develop convection correlations for perimeter zones with highly glazed spaces served by overhead slot-diffuser-based air systems. The following is for floors in such spaces.
Separate from the above model structure, there are also other comprehensive algorithm structures which are described below.
TARP Algorithm[LINK]
The comprehensive natural convection model, accessed using the keyword “TARP,” correlates the convective heat transfer coefficient to the surface orientation and the difference between the surface and zone air temperatures (where T = Surface Temperature - Air Temperature). The algorithm is taken directly from Walton (1983). Walton derived his algorithm from ASHRAE literature which can now be found for example in the ASHRAE Handbook (HoF 2001), Table 5 on p. 3.12, which gives equations for natural convection heat transfer coefficients in the turbulent range for large, vertical plates and for large, horizontal plates facing upward when heated (or downward when cooled). A note in the text also gives an approximation for large, horizontal plates facing downward when heated (or upward when cooled) recommending that it should be half of the facing upward value. Walton adds a curve fit as a function of the cosine of the tilt angle to provide intermediate values between vertical and horizontal. The curve fit values at the extremes match the ASHRAE values very well.
For no temperature difference OR a vertical surface the following correlation is used:
For (T < 0.0 AND an upward facing surface) OR (T > 0.0 AND an downward facing surface) an enhanced convection correlation is used:
where is the surface tilt angle.
For (T > 0.0 AND an upward facing surface) OR (T < 0.0 AND an downward facing surface) a reduced convection correlation is used:
where is the surface tilt angle.
Simple Natural Convection Algorithm[LINK]
The simple convection model uses constant coefficients for different heat transfer configurations, using the same criteria as the detailed model to determine reduced and enhanced convection. The coefficients are also taken directly from Walton (1983). Walton derived his coefficients from the surface conductances for =0.90 found in the ASHRAE Handbook (1985) in Table 1 on p. 23.2. The radiative heat transfer component was estimated at 1.02 * 0.9 = 0.918 BTU/h-ft2-F and then subtracted off. Finally the coefficients were converted to SI units to yield the values below.
For a vertical surface:
For a horizontal surface with reduced convection:
For a horizontal surface with enhanced convection:
For a tilted surface with reduced convection:
For a tilted surface with enhanced convection:
Ceiling Diffuser Algorithm[LINK]
The ceiling diffuser algorithm is based on empirical correlations developed by Fisher and Pedersen (1997). The correlation was reformulated to use the room outlet temperature as the reference temperature. The correlations are shown below.
For Floors:
The correlation for floors is illustrated in the following figure:
For ceilings:
The correlation for ceilings is illustrated in the following figure:
For Walls:
The correlation for walls is illustrated in the following figure:
Trombe Wall Algorithm[LINK]
The Trombe wall algorithm is used to model convection in a “Trombe wall zone”, i.e. the air space between the storage wall surface and the exterior glazing. (See the later sections on Passive and Active Trombe Walls below for more information about Trombe walls.) The algorithm is identical to the convection model (based on ISO 15099) used in Window5 for convection between glazing layers in multi-pane window systems. The use of the algorithm for modeling an unvented Trombe wall has been validated against experimental data by Ellis (2003).
This algorithm gives the convection coefficients for air in a narrow vertical cavity that is sealed and not ventilated. This applies both to the air gap in between panes of a window or to the air gap between the Trombe wall glazing and the inner surface (often a selective surface). These convection coefficients are really the only difference between a normal zone and a Trombe zone. The rest of the zone heat balance is the same, e.g., transmitted solar, long-wave radiation between surfaces, etc.
For a vertical cavity, the correlation from ISO 15099 is:
where
Nu = Nusselt number
Ra = Rayleigh number
A = aspect ratio of cavity
This is then used in EnergyPlus as follows:
Net convection coefficient from glazing to wall is:
where
k = conductivity of air
L = air gap thickness
Convection coefficient applied to each wall separately and actually used in the zone heat balance is:
References[LINK]
Alamdari, F. and G.P. Hammond. 1983. Improved data correlations for buoyancy-driven convection in rooms. Building Services Engineering Research & Technology. Vol. 4, No. 3.
ASHRAE. 1985. 1985 ASHRAE Handbook – Fundamentals, Atlanta: American Society of Heating, Refrigerating, and Air-Conditioning Engineers, Inc.
ASHRAE. 2001. 2001 ASHRAE Handbook – Fundamentals, Atlanta: American Society of Heating, Refrigerating, and Air-Conditioning Engineers, Inc.
Awbi, H.B. and A. Hatton. 1999. Natural convection from heated room surfaces. Energy and Buildings 30 (1999) 233-244.
Beausoleil-Morrison, I. 2000. The adaptive coupling of heat and air flow modeling within dynamic whole-building simulations. PhD. Thesis. University of Strathclyde, Glasgow, UK.
Ellis, Peter G. 2003. Development and Validation of the Unvented Trombe Wall Model in EnergyPlus. Master’s Thesis, University of Illinois at Urbana-Champaign.
Fisher, D.E. and C.O. Pedersen. 1997. “Convective Heat Transfer in Building Energy and Thermal Load Calculations”, ASHRAE Transactions, Vol. 103, Pt. 2.
Fohanno, S., and G. Polidori. 2006. Modelling of natural convective heat transfer at an internal surface. Energy and Buildings 38 (2006) 548 - 553
Goldstein, K. and A. Novoselac. 2010. Convective Heat Transfer in Rooms With Ceiling Slot Diffusers (RP-1416). HVAC&R Research Journal TBD
Karadag, R. 2009. New approach relevant to total heat transfer coefficient including the effect of radiation and convection at the ceiling in a cooled ceiling room. Applied Thermal Engineering 29 (2009) 1561-1565
Khalifa AJN. 1989. Heat transfer processes in buildings. Ph.D. Thesis, University of Wales College of Cardiff, Cardiff, UK.
ISO. 2003. ISO 15099:2003. Thermal performance of windows, doors, and shading devices – Detailed calculations. International Organization for Standardization.
Walton, G. N. 1983. Thermal Analysis Research Program Reference Manual. NBSSIR 83-2655. National Bureau of Standards (now NIST). This is documentation for “TARP.”
Documentation content copyright © 1996-2014 The Board of Trustees of the University of Illinois and the Regents of the University of California through the Ernest Orlando Lawrence Berkeley National Laboratory. All rights reserved. EnergyPlus is a trademark of the US Department of Energy.
This documentation is made available under the EnergyPlus Open Source License v1.0.