Evaporative Coolers[LINK]
This section describes the evaporative coolers models for HVAC in EnergyPlus.
Direct Evaporative Cooler[LINK]
The input object EvaporativeCooler:Direct:CelDekPad provides a model of a direct stage evaporative cooler, shown in the figure below, that consists of a rigid media evaporative pad, with water recirculated from a reservoir. The water is pumped from the reservoir to a water distribution header, for water feed by gravity from above the media. The evaporative pad provides the area for the adiabatic saturation of the air. While the process provides a lower dry-bulb temperature, the moisture content of the leaving air is higher than the entering condition. The direct stage is used for comfort cooling in a building where adding humidity to the air can be tolerated.
The thermodynamic process is a simultaneous heat and mass transfer, or adiabatic cooling, and follows a constant enthalpy line on the psychrometric chart; it is shown in the figure below as a process from A to B. Since the deviation of the constant wet-bulb line and the constant enthalpy line is small, it is assumed that the wet-bulb temperature is constant across the direct evaporative stage.
If the direct evaporative process were 100% efficient, the leaving dry-bulb temperature would equal the entering wet-bulb temperature. The efficiency of the direct evaporative process is less than 100% and by defining saturation efficiency (se) for the direct stage or evaporative pad, the leaving dry-bulb temperature can be expressed by the following equation.
Saturation Efficiency[LINK]
Since the evaporative process is not 100% efficient the saturation efficiency is defined by.
The saturation efficiency is determined from manufacturer’s data, and the least squares curve fit is discussed in Curve Fitting Evaporative Media section.
Using the saturation efficiency (se) for the direct stage evaporative pad, the leaving dry-bulb temperature can be determined directly. The evaporative process approximately follows a constant wet-bulb line. Therefore, with the leaving dry-bulb temperature and assuming adiabatic heat transfer across the direct stage, the outlet conditions for the direct stage are known.
The saturation efficiency of the direct evaporative cooler is a function of the pad geometry and airflow rate. The pad geometry is constant throughout the simulation, but the airflow rate can change from hour to hour when the evaporative cooler is used with an air economizer. The saturation efficiency would then be determined from the flow for that hour with the geometry of the direct evaporative cooler. This gives the dry-bulb temperature leaving the evaporative cooler. Assuming adiabatic heat transfer across the direct stage, the evaporative process follows the constant wet-bulb line or the constant enthalpy line on the psychrometric chart, therefore the wet-bulb temperature is constant from inlet to outlet.
Some things that can cause departure from the ideal adiabatic saturation process in the direct evaporative cooler are:
- makeup water entering the sump,
- friction from water re-circulation,
- heat transfer from surroundings,
- solar radiation (sun upon a cooler).
Thus, adiabatic saturation in evaporative cooling is only an approximation, however the adiabatic saturation assumption in the rigid-media cooler is good, since the water recirculates rapidly and approximates the wet-bulb temperature at steady state operation.
The saturation efficiency is usually reported as a function of airflow, pad face velocity, and pad thickness. The Figure below shows a typical graph of manufacturer’s data for the saturation efficiency. A multi-variate least squares curve fit of the data was used to generate saturation efficiency functions for the evaporative models that use the CelDek rigid media pad.
The curve fit for saturation efficiency was obtained using the functions listed below. The model uses the air velocity (Airvel) through the pad and the depth of the media (Depth). The least squares routine produced the following model that is used for the evaporative cooling rigid media pad. The least squares routine produced an eleven-term multi-variate fit using a third order quadratic.
se =0.792714 + 0.958569 (Depth) - 0.25193 (Airvel) - 1.03215 (Depth2) + 0.0262659 (Airvel2) + 0.914869 (Depth * Airvel) - 1.48241 (Airvel * Depth2) - 0.018992 (Airvel3 * Depth) + 1.13137 (Depth3*^^Airvel) + 0.0327622 (Airvel3*Depth2) - 0.145384 (Depth3*Airvel2)
Where Airvel is in meters per second and Depth is in meters. This curve fit is used for the rigid media in the EvapCooler:Direct:CelDekPad and EvapCooler:InDirect:CelDekPad.
Dry Coil Indirect Evaporative Cooler[LINK]
The input object EvaporativeCooler:Indirect:CelDekPad provides a model of a dry coil indirect evaporative cooler, shown in the figure below, that has a rigid media pad, similar to the direct evaporative stage, where the adiabatic cooling takes place. The secondary air leaves the rigid media pad and enters an air-to-air heat exchanger where it cools the supply air flowing through the heat exchanger tubes. The moist secondary air is then exhausted to the environment. The secondary air stream has its own fan and includes consists of a rigid media evaporative pad, with water recirculated from a reservoir. The water is pumped from the reservoir to a water distribution header, for water feed by gravity from above the media. The evaporative pad provides the area for the adiabatic saturation of the air.
The process that the secondary air goes through, A to C to D, is shown by the dashed lines in the following figure. Process A to C is adiabatic cooling in the rigid media pad. Then the air enters the shell side of the heat exchanger and is sensibly heated from C to D by the warm supply air passing through the tube side.
The advantage of the dry coil heat exchanger is that the heat exchanger does not have the evaporation taking place on the outside of the tubes, thus no mineral deposits are left on the heat exchange surface to reduce the efficiency of the heat exchanger. The rigid media pads are designed to flush the mineral deposits to the sump, so the saturation efficiency of the pad stays relatively constant.
The following equations are used to determine the dry-bulb temperature leaving the evaporative media, given pad geometry and secondary airflow information. The heat transfer in the heat exchanger can be determined with the effectiveness of the heat exchanger according.
Tdb sup out = Tdb sup in - se*(Todb - Towb )
QHx = Hx * Min( CFMsec , CFMsupply) * air * cp air * ( Todb - Tdb sec out )
After the heat transfer for the heat exchanger has been determined, an energy balance is done on the supply airside to determine the dry-bulb temperature leaving the indirect evaporative cooler. This assumes all the energy for is provided by the primary air stream so the effectiveness value includes the air-to-air effectiveness of the heat exchanger.
Tdb sup out = Tdb sup in -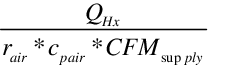 
The wet-bulb temperature is determined from psychrometric routines using the leaving dry-bulb temperature, humidity ratio, and barometric pressure, since humidity ratio is constant for the supply air across the indirect stage. The effectiveness of the heat exchanger is determined from a parameter estimation using manufacturer’s performance data. For the indirect evaporative cooler it was found that a value of 0.67 represented reasonable default effectiveness.
Wet Coil Indirect Evaporative Cooler[LINK]
The input object EvaporativeCooler:Indirect:WetCoil provides a model for a wetted coil evaporative cooler, shown in the figure below, that has water sprayed directly on the tubes of the heat exchanger where latent cooling takes place. The vaporization of the water on the outside of the heat exchanger tubes allows the simultaneous heat and mass transfer which removes heat from the supply air on the tube side. Then the moist secondary air is exhausted. The secondary air stream has its own fan.
The process that the secondary air goes through, A to C on the following figure, is a path of simultaneous heat and mass transfer, but it does not follow a line of constant enthalpy as in the direct stage. The process is not adiabatic due to the heat gain from the supply air flowing through the tubes of the heat exchanger.
The wet coil heat exchanger can have a higher stage efficiency than the dry coil due to a higher heat transfer rate on the outside of the heat exchanger tubes. Over the operating lifetime of the heat exchanger, the vaporization taking place on the heat exchange surface can leave mineral deposits that will decrease the effectiveness of the heat exchanger.
Efficiencies of the Indirect Stage[LINK]
In an indirect stage of an evaporative cooler, the secondary or wet side air stream acts as a heat sink for the supply air. The efficiency of the indirect stage is given as the effectiveness of the sensible heat exchange, Hx, and the saturation efficiency on the wet streamside, se. These are expressed as:
Hx =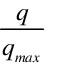 
= 
,
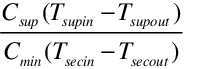se = 
,
where Tdb sup in = Tdb sec in for the indirect cooler. The maximum heat transfer possible would be obtained if the supply stream was cooled all the way to the wet-bulb temperature. So the efficiency of the indirect evaporative cooler is defined by:
ind =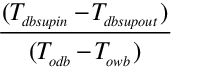 
.
Using the combination of the effectiveness and saturation efficiency, the total efficiency of the indirect stage can be expressed by:
ind = Hx se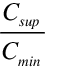 
.
In many cases Csup = Cmin and the efficiency of the indirect stage reduces to:
ind = Hx se.
An intuitive model determining the performance of the wet coil indirect model was developed. This model can be used for all indirect models by curve fitting data from the evaporative cooler of interest. The model development starts with the total efficiency of the indirect evaporative cooler:
ind =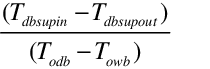 
Solving for T db sup out gives the leaving conditions of the supply air at a constant humidity ratio:
T db sup out = Tdb sup in - ind * (Todb - Towb)
A form for the efficiency of the indirect stage was devised using a maximum efficiency with a coefficient to reduce the efficiency depending on the ratio of the airflows.
ind = max - C1 * (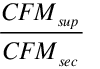
)
C1 is the “Flow Efficiency Ratio” and is determined from performance data.
A check of limits will verify that it makes physical sense. As the magnitude of the secondary flow increases, the second term of equation above becomes smaller. This would make the efficiency tend to go to the maximum efficiency. Physically this would be true since the convective terms for heat and mass transfer would increase on the outside of the tube with the additional mass flow rate. Similarly, if the supply air flow goes to zero with a constant secondary air flow, the second term of the equation above again becomes small, and the overall efficiency of the stage would approach the maximum. The constant C1 tells how quickly the efficiency of the stage would decrease with a mismatch of the supply and secondary flows.
The maximum efficiency of the stage is a combination of the efficiency due to the simultaneous heat and mass transfer on the outside of the tube and the efficiency of the heat exchanger. This value can be higher than the dry coil overall efficiency since the convective coefficients on the outside of the tube are larger. For example, a least squares fit for the maximum efficiency showed this value was approximately 0.8 compared to the dry coil indirect value of approximately 0.65 (0.67 * 0.97). (The maximum efficiency for the dry coil indirect was determined at the condition where flow through the evaporative pad in the secondary air stream approached zero, for a 12-inch thick pad.) It should be noted again that over the operating life of the wet coil heat exchanger, the mineral deposits that are left can decrease the effectiveness of the heat exchanger unless appropriate maintenance has taken place. Therefore, if modeling an older system, the manufacturer’s data may no longer describe the equipment effectiveness.
Two Stage Direct/Indirect Evaporative Cooler[LINK]
A two stage cooler can be modeled by combining either a wet coil or the dry coil indirect evaporative cooler staged with a direct evaporative cooler. The figure below shows a dry coil indirect evaporative cooler with a direct evaporative cooler. This configuration is mainly used for total comfort cooling for a building and would not normally be used as a pre-cooler for a refrigeration coil, since the direct stage would increase the latent load on a refrigeration coil.
The thermodynamic process for the supply air is shown below, going from A to B to C. The process from A to B is sensible cooling in the indirect stage. The process from B to C is simultaneous heat and mass transfer following a constant enthalpy line. The air leaving the final stage has a lower dry-bulb and wet-bulb temperature, and an increase in moisture from the direct stage.
Two stage evaporative coolers can be accomplished by putting the EvaporativeCooler:Direct:CelDekPad, EvaporativeCooler:Indirect:CelDekPad, EvaporativeCooler:Indirect:WetCoil in series in any combination the user desires in the supply air loop.
Indirect Evaporative Cooler Special Research Model[LINK]
This section summarizes the model implemented in the component EvaporativeCooler:Indirect:ResearchSpecial. Examples of this evaporative cooler are shown in the following figures, without and with a relief valve. This model differs from the other indirect evaporative coolers in that, under part load conditions, it can modulate so that the air leaving the cooler just meets a drybulb temperature setpoint. It is also a simple model with a constant effectiveness.
The algorithm used to determine the cooling provided to the system air proceeds in these three steps:
- calculate full load performance using PLF=1 and Equation and Equation
- calculate PLF using Equation , Equation , and Equation , and
- recalculate performance using PLF from step 2.
- If PLF = 1 then use Equation and Equation
- If PLF <1 then outlet temp = desired outlet temp (as by magic)
- Auxiliary fan energy adjusted by PLF
- Water consumption based on change in enthalpy in air system
where,
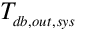is the dry-bulb of the system air leaving the cooler [ºC]
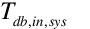is the dry-bulb of the system air entering the cooler [ºC]
is a cooler effectiveness (eg. 0.7 to 1.2)
is the wet-bulb of the purge air entering the wet side of cooler [ºC]
The purge air, or secondary airside, is the stream that evaporates water and indirectly cools the primary, or system air. The result from Equation is then compared to a lower bound,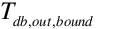 
, determined from the dewpoint of the incoming purge air using Equation .
where,
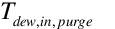is the dewpoint of purge air entering the wet side of cooler [ºC]
is a factor for how close to dewpoint is possible (eg. 0.9)
The final result (for PLF = 1) is the larger of the results from Equations and .
The indirect cooler has the ability to overcool the air and therefore needs some form of modulation. A Part Load Fraction, PLF, is used to model the implications of controlling the amount of cooling. It is assumed that through on/off cycling that the cooling power can be varied to exactly meet the desired temperature when PLF is less than unity. The auxiliary fan power is then varied linearly using a Part Load Fraction.
where,
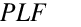is the Part Load Fraction
When PLF is less than 1.0 it is assumed that the cooler will deliver the desired temperature air (as long as it is less than the inlet; it doesn’t need heating). The PLF is used to modify the auxiliary fan power and find when the unit will overcool.
Water pump power is also derated using the PLF.
A third air stream input to the cooler was implemented in order to allow mixing building exhaust air with outdoor air on the purge/secondary side of the cooler. The assumption when relief/tertiary air is used is that all of the available relief zone air is used and the remainder made up with outdoor air. Moisture and energy balances are drawn to compute humidity ratio and enthalpy of mixed secondary air. The volume is determined by the design volume flow rate (from secondary fan size).
Water Consumption[LINK]
Water consumption is an important consideration when evaluating evaporative coolers. Water consumption of the evaporative cooler is modeled using Equation .
The three components of water consumption are evaporation, drift, and blowdown. Evaporation is the water evaporated as the normal part of the evaporative cooler thermodynamic process and is calculated using:
where,
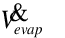is the volume flow rate of useful water evaporation [m3/s]
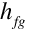is the heat of vaporization of water (taken as 2,500,000 J/kg)
is the rate of heat transfer calculated as by Equation or Equation [W]
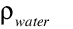is the density of water [kg/m3]
Drift is water that leaves the secondary side as droplets and does not contribute to the evaporative cooling process in a useful manner. It is calculated using a user input factor that describes drift as a fraction of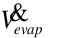 
.
Blowdown is water drained from the sump to counter the build up of solids in the water that would otherwise occur because of evaporation. It is calculated using a user input factor for the blowdown concentration ratio ,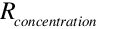
, which is the ratio of solids in in the blowdown water compared to the solids in the fresh makeup water and is limited to values of 2 or higher. The make up water needed for blowdown is calculated using:
Direct Evaporative Cooler Special Research Model[LINK]
This section summarizes the model implemented in the component EvaporativeCooler:Direct:ResearchSpecial. This is a simple constant effectiveness model that, under part load conditions, can modulate so that the air leaving the cooler just meets a drybulb temperature setpoint. The algorithm used to determine the changes to the system air proceeds in three steps:
- calculate full load performance using a part load fraction (PLF)=1 and Equation .
- calculate PLF using Equations , , and .
- recalculate cooler performance using the PLF.
where,
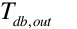is the drybub temperature of the air leaving the cooler [ºC],
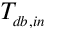is the drybulb temperature of the air entering the cooler [ºC],
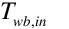is the wetbulb temperature of the air entering the cooler [ºC], and
is the cooler effectiveness.
The wetbulb temperature of air leaving a direct cooler is the same as the wetbulb temperature entering the cooler. The leaving humidity ratio of the air is calculated using psychrometric functions with with leaving drybulb and wetbulb temperatures and outdoor air pressure as inputs. The leaving enthalpy of air is calculated using pyschrometric functions with leaving drybulb temperature, leaving humidity ratio, and outdoor air pressure as inputs.
The direct cooler sometimes has the ability to overcool the air and therefore some form of modulation is useful for analysis. The special research model includes a Part Load Fraction, PLF, used to model the implications of controlling the amount of cooling. It is assumed that through some sort of on/off cycling or wetness control that the cooling power can be varied to exactly meet the desired temperature when PLF is less than unity. The auxiliary water pump power is then varied linearly using a Part Load Fraction.
When PLF is less than 1.0 it is assumed that the cooler will deliver the desired temperature air (as long as it is less than the inlet; it doesn’t need heating). Water pump power is also derated using the PLF.
Water Consumption[LINK]
Water consumption is an important consideration when evaluating evaporative coolers. Water consumption of the evaporative cooler is modeled using Equation .
The three components of water consumption are evaporation, drift, and blowdown. Evaporation is the water evaporated as the normal part of the evaporative cooler thermodynamic process and is calculated using:
where,
is the volume flow rate of useful water evaporation [m3/s]
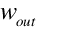is the humidity ratio of the air leaving the cooler [kg/kg]
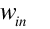is the humidity ratio of air entering the cooler [kg/kg]
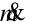is the mass flow rate of air moving through the cooler [kg/s]
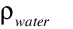is the density of water [kg/m3]
Drift is water that leaves the cooler (and supply air duct) as droplets and does not contribute to the evaporative cooling process in a useful manner. It is calculated using a user input factor that describes drift as a fraction of 
.
Blowdown is water drained from the sump to counter the build up of solids in the water that would otherwise occur because of evaporation. It is calculated using a user input factor for the blowdown concentration ratio ,
, which is the ratio of solids in the blowdown water compared to the solids in the fresh makeup water and is limited to values of 2 or higher. The make up water needed for blowdown is calculated using:
Evaporative Coolers[LINK]
This section describes the evaporative coolers models for HVAC in EnergyPlus.
Direct Evaporative Cooler[LINK]
The input object EvaporativeCooler:Direct:CelDekPad provides a model of a direct stage evaporative cooler, shown in the figure below, that consists of a rigid media evaporative pad, with water recirculated from a reservoir. The water is pumped from the reservoir to a water distribution header, for water feed by gravity from above the media. The evaporative pad provides the area for the adiabatic saturation of the air. While the process provides a lower dry-bulb temperature, the moisture content of the leaving air is higher than the entering condition. The direct stage is used for comfort cooling in a building where adding humidity to the air can be tolerated.
The thermodynamic process is a simultaneous heat and mass transfer, or adiabatic cooling, and follows a constant enthalpy line on the psychrometric chart; it is shown in the figure below as a process from A to B. Since the deviation of the constant wet-bulb line and the constant enthalpy line is small, it is assumed that the wet-bulb temperature is constant across the direct evaporative stage.
If the direct evaporative process were 100% efficient, the leaving dry-bulb temperature would equal the entering wet-bulb temperature. The efficiency of the direct evaporative process is less than 100% and by defining saturation efficiency (se) for the direct stage or evaporative pad, the leaving dry-bulb temperature can be expressed by the following equation.
Saturation Efficiency[LINK]
Since the evaporative process is not 100% efficient the saturation efficiency is defined by.
The saturation efficiency is determined from manufacturer’s data, and the least squares curve fit is discussed in Curve Fitting Evaporative Media section.
Using the saturation efficiency (se) for the direct stage evaporative pad, the leaving dry-bulb temperature can be determined directly. The evaporative process approximately follows a constant wet-bulb line. Therefore, with the leaving dry-bulb temperature and assuming adiabatic heat transfer across the direct stage, the outlet conditions for the direct stage are known.
The saturation efficiency of the direct evaporative cooler is a function of the pad geometry and airflow rate. The pad geometry is constant throughout the simulation, but the airflow rate can change from hour to hour when the evaporative cooler is used with an air economizer. The saturation efficiency would then be determined from the flow for that hour with the geometry of the direct evaporative cooler. This gives the dry-bulb temperature leaving the evaporative cooler. Assuming adiabatic heat transfer across the direct stage, the evaporative process follows the constant wet-bulb line or the constant enthalpy line on the psychrometric chart, therefore the wet-bulb temperature is constant from inlet to outlet.
Some things that can cause departure from the ideal adiabatic saturation process in the direct evaporative cooler are:
Thus, adiabatic saturation in evaporative cooling is only an approximation, however the adiabatic saturation assumption in the rigid-media cooler is good, since the water recirculates rapidly and approximates the wet-bulb temperature at steady state operation.
Curve Fitting Evaporative Media[LINK]
The saturation efficiency is usually reported as a function of airflow, pad face velocity, and pad thickness. The Figure below shows a typical graph of manufacturer’s data for the saturation efficiency. A multi-variate least squares curve fit of the data was used to generate saturation efficiency functions for the evaporative models that use the CelDek rigid media pad.
The curve fit for saturation efficiency was obtained using the functions listed below. The model uses the air velocity (Airvel) through the pad and the depth of the media (Depth). The least squares routine produced the following model that is used for the evaporative cooling rigid media pad. The least squares routine produced an eleven-term multi-variate fit using a third order quadratic.
se =0.792714 + 0.958569 (Depth) - 0.25193 (Airvel) - 1.03215 (Depth2) + 0.0262659 (Airvel2) + 0.914869 (Depth * Airvel) - 1.48241 (Airvel * Depth2) - 0.018992 (Airvel3 * Depth) + 1.13137 (Depth3*^^Airvel) + 0.0327622 (Airvel3*Depth2) - 0.145384 (Depth3*Airvel2)
Where Airvel is in meters per second and Depth is in meters. This curve fit is used for the rigid media in the EvapCooler:Direct:CelDekPad and EvapCooler:InDirect:CelDekPad.
Dry Coil Indirect Evaporative Cooler[LINK]
The input object EvaporativeCooler:Indirect:CelDekPad provides a model of a dry coil indirect evaporative cooler, shown in the figure below, that has a rigid media pad, similar to the direct evaporative stage, where the adiabatic cooling takes place. The secondary air leaves the rigid media pad and enters an air-to-air heat exchanger where it cools the supply air flowing through the heat exchanger tubes. The moist secondary air is then exhausted to the environment. The secondary air stream has its own fan and includes consists of a rigid media evaporative pad, with water recirculated from a reservoir. The water is pumped from the reservoir to a water distribution header, for water feed by gravity from above the media. The evaporative pad provides the area for the adiabatic saturation of the air.
The process that the secondary air goes through, A to C to D, is shown by the dashed lines in the following figure. Process A to C is adiabatic cooling in the rigid media pad. Then the air enters the shell side of the heat exchanger and is sensibly heated from C to D by the warm supply air passing through the tube side.
The advantage of the dry coil heat exchanger is that the heat exchanger does not have the evaporation taking place on the outside of the tubes, thus no mineral deposits are left on the heat exchange surface to reduce the efficiency of the heat exchanger. The rigid media pads are designed to flush the mineral deposits to the sump, so the saturation efficiency of the pad stays relatively constant.
The following equations are used to determine the dry-bulb temperature leaving the evaporative media, given pad geometry and secondary airflow information. The heat transfer in the heat exchanger can be determined with the effectiveness of the heat exchanger according.
Tdb sup out = Tdb sup in - se*(Todb - Towb )
QHx = Hx * Min( CFMsec , CFMsupply) * air * cp air * ( Todb - Tdb sec out )
After the heat transfer for the heat exchanger has been determined, an energy balance is done on the supply airside to determine the dry-bulb temperature leaving the indirect evaporative cooler. This assumes all the energy for is provided by the primary air stream so the effectiveness value includes the air-to-air effectiveness of the heat exchanger.
Tdb sup out = Tdb sup in -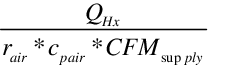
The wet-bulb temperature is determined from psychrometric routines using the leaving dry-bulb temperature, humidity ratio, and barometric pressure, since humidity ratio is constant for the supply air across the indirect stage. The effectiveness of the heat exchanger is determined from a parameter estimation using manufacturer’s performance data. For the indirect evaporative cooler it was found that a value of 0.67 represented reasonable default effectiveness.
Wet Coil Indirect Evaporative Cooler[LINK]
The input object EvaporativeCooler:Indirect:WetCoil provides a model for a wetted coil evaporative cooler, shown in the figure below, that has water sprayed directly on the tubes of the heat exchanger where latent cooling takes place. The vaporization of the water on the outside of the heat exchanger tubes allows the simultaneous heat and mass transfer which removes heat from the supply air on the tube side. Then the moist secondary air is exhausted. The secondary air stream has its own fan.
The process that the secondary air goes through, A to C on the following figure, is a path of simultaneous heat and mass transfer, but it does not follow a line of constant enthalpy as in the direct stage. The process is not adiabatic due to the heat gain from the supply air flowing through the tubes of the heat exchanger.
The wet coil heat exchanger can have a higher stage efficiency than the dry coil due to a higher heat transfer rate on the outside of the heat exchanger tubes. Over the operating lifetime of the heat exchanger, the vaporization taking place on the heat exchange surface can leave mineral deposits that will decrease the effectiveness of the heat exchanger.
Efficiencies of the Indirect Stage[LINK]
In an indirect stage of an evaporative cooler, the secondary or wet side air stream acts as a heat sink for the supply air. The efficiency of the indirect stage is given as the effectiveness of the sensible heat exchange, Hx, and the saturation efficiency on the wet streamside, se. These are expressed as:
Hx =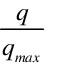
= 
,
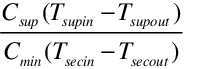se =
,
where Tdb sup in = Tdb sec in for the indirect cooler. The maximum heat transfer possible would be obtained if the supply stream was cooled all the way to the wet-bulb temperature. So the efficiency of the indirect evaporative cooler is defined by:
ind =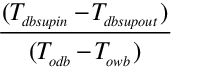
.
Using the combination of the effectiveness and saturation efficiency, the total efficiency of the indirect stage can be expressed by:
ind = Hx se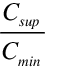
.
In many cases Csup = Cmin and the efficiency of the indirect stage reduces to:
ind = Hx se.
An intuitive model determining the performance of the wet coil indirect model was developed. This model can be used for all indirect models by curve fitting data from the evaporative cooler of interest. The model development starts with the total efficiency of the indirect evaporative cooler:
ind =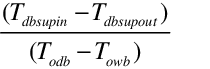
Solving for T db sup out gives the leaving conditions of the supply air at a constant humidity ratio:
T db sup out = Tdb sup in - ind * (Todb - Towb)
A form for the efficiency of the indirect stage was devised using a maximum efficiency with a coefficient to reduce the efficiency depending on the ratio of the airflows.
ind = max - C1 * (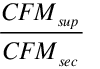
)
C1 is the “Flow Efficiency Ratio” and is determined from performance data.
A check of limits will verify that it makes physical sense. As the magnitude of the secondary flow increases, the second term of equation above becomes smaller. This would make the efficiency tend to go to the maximum efficiency. Physically this would be true since the convective terms for heat and mass transfer would increase on the outside of the tube with the additional mass flow rate. Similarly, if the supply air flow goes to zero with a constant secondary air flow, the second term of the equation above again becomes small, and the overall efficiency of the stage would approach the maximum. The constant C1 tells how quickly the efficiency of the stage would decrease with a mismatch of the supply and secondary flows.
The maximum efficiency of the stage is a combination of the efficiency due to the simultaneous heat and mass transfer on the outside of the tube and the efficiency of the heat exchanger. This value can be higher than the dry coil overall efficiency since the convective coefficients on the outside of the tube are larger. For example, a least squares fit for the maximum efficiency showed this value was approximately 0.8 compared to the dry coil indirect value of approximately 0.65 (0.67 * 0.97). (The maximum efficiency for the dry coil indirect was determined at the condition where flow through the evaporative pad in the secondary air stream approached zero, for a 12-inch thick pad.) It should be noted again that over the operating life of the wet coil heat exchanger, the mineral deposits that are left can decrease the effectiveness of the heat exchanger unless appropriate maintenance has taken place. Therefore, if modeling an older system, the manufacturer’s data may no longer describe the equipment effectiveness.
Two Stage Direct/Indirect Evaporative Cooler[LINK]
A two stage cooler can be modeled by combining either a wet coil or the dry coil indirect evaporative cooler staged with a direct evaporative cooler. The figure below shows a dry coil indirect evaporative cooler with a direct evaporative cooler. This configuration is mainly used for total comfort cooling for a building and would not normally be used as a pre-cooler for a refrigeration coil, since the direct stage would increase the latent load on a refrigeration coil.
The thermodynamic process for the supply air is shown below, going from A to B to C. The process from A to B is sensible cooling in the indirect stage. The process from B to C is simultaneous heat and mass transfer following a constant enthalpy line. The air leaving the final stage has a lower dry-bulb and wet-bulb temperature, and an increase in moisture from the direct stage.
Two stage evaporative coolers can be accomplished by putting the EvaporativeCooler:Direct:CelDekPad, EvaporativeCooler:Indirect:CelDekPad, EvaporativeCooler:Indirect:WetCoil in series in any combination the user desires in the supply air loop.
Indirect Evaporative Cooler Special Research Model[LINK]
This section summarizes the model implemented in the component EvaporativeCooler:Indirect:ResearchSpecial. Examples of this evaporative cooler are shown in the following figures, without and with a relief valve. This model differs from the other indirect evaporative coolers in that, under part load conditions, it can modulate so that the air leaving the cooler just meets a drybulb temperature setpoint. It is also a simple model with a constant effectiveness.
The algorithm used to determine the cooling provided to the system air proceeds in these three steps:
where,
The purge air, or secondary airside, is the stream that evaporates water and indirectly cools the primary, or system air. The result from Equation is then compared to a lower bound,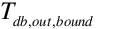
, determined from the dewpoint of the incoming purge air using Equation .
where,
The final result (for PLF = 1) is the larger of the results from Equations and .
The indirect cooler has the ability to overcool the air and therefore needs some form of modulation. A Part Load Fraction, PLF, is used to model the implications of controlling the amount of cooling. It is assumed that through on/off cycling that the cooling power can be varied to exactly meet the desired temperature when PLF is less than unity. The auxiliary fan power is then varied linearly using a Part Load Fraction.
where,
When PLF is less than 1.0 it is assumed that the cooler will deliver the desired temperature air (as long as it is less than the inlet; it doesn’t need heating). The PLF is used to modify the auxiliary fan power and find when the unit will overcool.
Water pump power is also derated using the PLF.
A third air stream input to the cooler was implemented in order to allow mixing building exhaust air with outdoor air on the purge/secondary side of the cooler. The assumption when relief/tertiary air is used is that all of the available relief zone air is used and the remainder made up with outdoor air. Moisture and energy balances are drawn to compute humidity ratio and enthalpy of mixed secondary air. The volume is determined by the design volume flow rate (from secondary fan size).
Water Consumption[LINK]
Water consumption is an important consideration when evaluating evaporative coolers. Water consumption of the evaporative cooler is modeled using Equation .
The three components of water consumption are evaporation, drift, and blowdown. Evaporation is the water evaporated as the normal part of the evaporative cooler thermodynamic process and is calculated using:
where,
Drift is water that leaves the secondary side as droplets and does not contribute to the evaporative cooling process in a useful manner. It is calculated using a user input factor that describes drift as a fraction of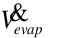
.
Blowdown is water drained from the sump to counter the build up of solids in the water that would otherwise occur because of evaporation. It is calculated using a user input factor for the blowdown concentration ratio ,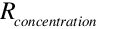
, which is the ratio of solids in in the blowdown water compared to the solids in the fresh makeup water and is limited to values of 2 or higher. The make up water needed for blowdown is calculated using:
Direct Evaporative Cooler Special Research Model[LINK]
This section summarizes the model implemented in the component EvaporativeCooler:Direct:ResearchSpecial. This is a simple constant effectiveness model that, under part load conditions, can modulate so that the air leaving the cooler just meets a drybulb temperature setpoint. The algorithm used to determine the changes to the system air proceeds in three steps:
where,
The wetbulb temperature of air leaving a direct cooler is the same as the wetbulb temperature entering the cooler. The leaving humidity ratio of the air is calculated using psychrometric functions with with leaving drybulb and wetbulb temperatures and outdoor air pressure as inputs. The leaving enthalpy of air is calculated using pyschrometric functions with leaving drybulb temperature, leaving humidity ratio, and outdoor air pressure as inputs.
The direct cooler sometimes has the ability to overcool the air and therefore some form of modulation is useful for analysis. The special research model includes a Part Load Fraction, PLF, used to model the implications of controlling the amount of cooling. It is assumed that through some sort of on/off cycling or wetness control that the cooling power can be varied to exactly meet the desired temperature when PLF is less than unity. The auxiliary water pump power is then varied linearly using a Part Load Fraction.
When PLF is less than 1.0 it is assumed that the cooler will deliver the desired temperature air (as long as it is less than the inlet; it doesn’t need heating). Water pump power is also derated using the PLF.
Water Consumption[LINK]
Water consumption is an important consideration when evaluating evaporative coolers. Water consumption of the evaporative cooler is modeled using Equation .
The three components of water consumption are evaporation, drift, and blowdown. Evaporation is the water evaporated as the normal part of the evaporative cooler thermodynamic process and is calculated using:
where,
Drift is water that leaves the cooler (and supply air duct) as droplets and does not contribute to the evaporative cooling process in a useful manner. It is calculated using a user input factor that describes drift as a fraction of
.
Blowdown is water drained from the sump to counter the build up of solids in the water that would otherwise occur because of evaporation. It is calculated using a user input factor for the blowdown concentration ratio ,
, which is the ratio of solids in the blowdown water compared to the solids in the fresh makeup water and is limited to values of 2 or higher. The make up water needed for blowdown is calculated using:
Documentation content copyright © 1996-2014 The Board of Trustees of the University of Illinois and the Regents of the University of California through the Ernest Orlando Lawrence Berkeley National Laboratory. All rights reserved. EnergyPlus is a trademark of the US Department of Energy.
This documentation is made available under the EnergyPlus Open Source License v1.0.