Zone Equipment and Zone Forced Air Units[LINK]
Air Distribution Terminal Unit[LINK]
The ZoneHVAC:AirDistributionUnit is a special piece of zone equipment – it connects centrally conditioned air with a zone. It encompasses the various types of air terminal units in EnergyPlus: AirTerminal:DualDuct:ConstantVolume, AirTerminal:SingleDuct:VAV:Reheat, etc. It is a generalized component that accesses the calculations for the different types of air terminal unit.
The air distribution function is encapsulated in the module ZoneAirEquipmentManager. The object and module function only to invoke the individual air terminal unit simulations.
The data for this unit consists of the unit name, the air outlet node name (which should be the same as one of the zone inlet nodes), the type of air terminal unit (air distribution equipment), and the name of the air terminal unit.
All input data for air distribution units is stored in the array AirDistUnit in data module DataDefineEquip.
There is no calculation associated with ZoneHVAC:AirDistributionUnit.
Simulation and Control[LINK]
SimZoneAirLoopEquipment in module ZoneAirEquipmentManager calls the individual air terminal unit simulations.
No specific references.
Simple Duct Leakage Model[LINK]
The input object ZoneHVAC:AirDistributionUnit also provides access to a model for duct leakage that can be a significant source of energy inefficiency in forced-air HVAC systems. Evaluating duct leakage energy losses can involve considerable user effort and computer resources if an airflow network is defined through a detailed description of the system components and airflow paths (including leakage paths). A nonlinear pressure-based solver is used to solve for pressures and flow rates in the network. By making certain assumptions and approximations for certain well defined configurations, however, it is possible to obtain accurate results with a simple mass and energy balance calculation and thus avoid the input and calculation costs of doing a full pressure-based airflow network simulation.
The Simple Duct Leakage Model (SDLM) assumes a central VAV air conditioning system with a constant static pressure setpoint. The model assumes that the leaks are in the supply ducts and that the system returns air through a ceiling plenum that contains the ducts. Thus, the ducts leak into the return plenum, and this part of the supply does not reach the conditioned zones. With the additional assumptions described below, it is possible to model this configuration with heat and mass balance equations and avoid the use of a nonlinear pressure-based solver. In the EnergyPlus context, this means that use of AirflowNetwork is avoided and the leakage calculations are obtained in the course of the normal thermal simulation.
Principles and Description[LINK]
Constant Flow Rate
The airflow rate through a duct leak is a function of the pressure difference between the duct and the surrounding space:
The exponent n is 0.5 for leaks that look like orifices (holes that are large relative to the thickness of the duct wall); for leaks that resemble cracks (e.g., lap joints), n is approximately 0.6 to 0.65.
For a duct with constant flow rate and a linear pressure drop through the duct, the average static pressure in the duct will equal half of the duct static pressure drop. Assuming turbulent flow in the duct, the duct pressure drop is proportional to the square of the airflow through the duct. This can be expressed as:
Combining equations and and assuming the leaks are large holes (n equals 0.5). gives:
where
Thus the leakage fraction C3 remains constant regardless of the duct flow rate or static pressure. This result depends on the following assumptions:
the duct airflow is turbulent;
the duct pressure varies linearly along the duct;
the average duct pressure approximates the pressure drop across the duct;
the leaks are large and have pressure exponent 0.5.
Effects of Constant Pressure Upstream and Variable Flow and Pressure Downstrean
Commonly VAV systems maintain a constant static pressure at some point in the duct system upstream of the VAV terminal units. That is, airflow rate will vary depending on the cooling requirement, but a constant pressure will be maintained at the static pressure sensor. Consequently, the leakage flow for a leak upstream of the VAV boxes will be approximately constant. Or to put it another way, the leakage fraction will vary in proportion to the flow rate.
For leaks downstream of the VAV terminal units, the airflow through the duct and the pressure in the downstream duct will vary as the box damper modulates in response to the differential between the room temperature and the thermostat setpoint. In this case, the situation is similar to the constant flow case: for an orifice-like leak, the pressure difference across the leak will vary linearly with the air speed (or flow rate); i.e., the leakage fraction will be approximately constant.
SDLM
For SDLM, our leakage model is then:
for leaks upstream of the terminal units, the leakage flow rate will be constant;
for leaks downstream of the terminal units, the leakage fraction will be constant.
This model assumes, in addition to the assumptions given above, that the VAV system is controlled to a constant static pressure setpoint. In EnergyPlus SDLM is not currently applicable to systems using static pressure reset. Using SDLM would require knowledge of static pressure as a function of system air flow rate.
User data for the SDLM is entered through The ZoneHVAC:AirDistributionUnit (ADU) object. There are 2 data items per ADU:
the upstream nominal leakage fraction;
the downstream fixed leakage fraction.
Both inputs are leakage fractions. Input (1) is the leakage fraction at design flow rate, which together can be used to determine the constant leakage flow rate upstream of the VAV boxes; this leakage fraction varies with the flow rate. Input (2) is a fixed leakage fraction and is constant as the flow rate varies.
Implementation[LINK]
The various zone mass flow rates are related in the following manner.


Here
 is the constant zone supply air mass flow rate upstream of the leaks [kg/s];
is the constant zone supply air mass flow rate upstream of the leaks [kg/s];
 is the air mass flow rate through the terminal unit [kg/s];
is the air mass flow rate through the terminal unit [kg/s];
 is the upstream leakage air mass flow rate [kg/s];
is the upstream leakage air mass flow rate [kg/s];
 is the downstream leakage air mass flow rate [kg/s];
is the downstream leakage air mass flow rate [kg/s];
 is the maximum upstream supply air mass flow rate (program input) [kg/s];
is the maximum upstream supply air mass flow rate (program input) [kg/s];
 is the supply air mass flow rate delivered to the zone [kg/s];
is the supply air mass flow rate delivered to the zone [kg/s];
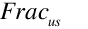 is the design upstream leakage fraction (program input);
is the design upstream leakage fraction (program input);
 is the constant downstream leakage fraction (program input);
is the constant downstream leakage fraction (program input);
 is calculated in the VAV terminal unit model in the usual manner: the mass flow rate is varied to meet the zone load. The limits on the mass flow rate variation are set by the
is calculated in the VAV terminal unit model in the usual manner: the mass flow rate is varied to meet the zone load. The limits on the mass flow rate variation are set by the  and
and  values stored at the terminal unit’s air inlet node. To account for upstream leakage the maximum air mass flow rate available is reset to:
values stored at the terminal unit’s air inlet node. To account for upstream leakage the maximum air mass flow rate available is reset to:
Downstream leakage must also be accounted for because not all of  will reach the zone. This is done by having
will reach the zone. This is done by having  meet an adjusted zone load:
meet an adjusted zone load:
Here 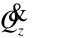 [watts] is the actual zone load (met by
[watts] is the actual zone load (met by  ) and
) and  is the load used in the VAV terminal unit model to obtain
is the load used in the VAV terminal unit model to obtain  .
.
Once 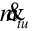 is known, all the other flow rates can be calculated.
is known, all the other flow rates can be calculated.  is assigned to the air distribution unit’s air inlet node and
is assigned to the air distribution unit’s air inlet node and  is assigned to the unit’s air outlet node. Thus, air mass flow is not conserved through the unit: the two air leakage flow rates disappear. These two vanished flow rates are stored in the air distribution unit data structure. When the downstream return air plenum mass and energy balances are calculated, the leakage flow rate data is accessed and added back in as inlets to the return air plenum. Thus, the overall air system preserves a mass balance.
is assigned to the unit’s air outlet node. Thus, air mass flow is not conserved through the unit: the two air leakage flow rates disappear. These two vanished flow rates are stored in the air distribution unit data structure. When the downstream return air plenum mass and energy balances are calculated, the leakage flow rate data is accessed and added back in as inlets to the return air plenum. Thus, the overall air system preserves a mass balance.
Wray, C.P. 2003. “Duct Thermal Performance Models for Large Commercial Buildings”, Lawrence Berkeley National Laboratory Report to the California Energy Commission. LBNL-53410.
Wray, C.P. and N.E. Matson. 2003. “Duct Leakage Impacts on VAV System Performance in California Large Commercial Buildings”, Lawrence Berkeley National Laboratory Report to the California Energy Commission. LBNL-53605.
Wray, C.P., R.C. Diamond, and M.H. Sherman. 2005. “Rationale for Measuring Duct Leakage Flows in Large Commercial Buildings”. Proceedings – 26th AIVC Conference, Brussels, Belgium, September. LBNL-58252.
Fan Coil Unit[LINK]
Window Air Conditioner[LINK]
Packaged Terminal Air Conditioner[LINK]
Packaged Terminal Heat Pump[LINK]
Zone Single Speed Water-To-Air Heat Pump[LINK]
The input object ZoneHVAC:WaterToAirHeatPump provides a zone equipment model for a water-to-air heat pump that is a “virtual” component consisting of an on/off fan component, a water-to-air heat pump cooling coil, a water-to-air heat pump heating coil, and a gas or electric supplemental heating coil. The specific configuration of the blowthru heat pump is shown in the following figure. For a drawthru heat pump, the fan is located between the water-to-air heat pump heating coil and the supplemental heating coil. In addition, a water-to-air heat pump has a water loop connection on its source side. The water loop can be served by a condenser loop (like GHE for Ground source systems), or by a cooling tower/ boiler plant loop (for water loop systems).
There are two models for zone water-to-air heat pump cooling and heating coils, i.e. Single-Speed and Variable-Speed Equation Fit models. Cooling and heating coils are modeled using the Equation Fit model described here.
Single Speed Equation-Fit Model:[LINK]
This section describes the equation-fit model for Water-to-Air heat pump (Object names: Coil:Cooling:WaterToAirHeatPump:EquationFit andCoil:Heating:WaterToAirHeatPump:EquationFit). This documentation is derived from the M.S. dissertation of Tang (2005) which is available on the Oklahoma State University web site http://www.hvac.okstate.edu/. The model uses five non-dimensional equations or curves to predict the heat pump performance in cooling and heating mode. The methodology involves using the generalized least square method to generate a set of performance coefficients from the catalog data at indicated reference conditions. Then the respective coefficients and indicated reference conditions are used in the model to simulate the heat pump performance. The variables or inlet conditions that influenced the water-to-air heat pump performance are load side inlet water temperature, source side inlet temperature, source side water flow rate and load side water flow rate. The governing equations for the cooling and heating mode are as following:
Cooling Mode:
Heating Mode:
Assuming no losses, the source side heat transfer rate for cooling and heating mode is calculated as following;
where:
 = Equation fit coefficients for the cooling and heating mode
= Equation fit coefficients for the cooling and heating mode
 = 283K
= 283K
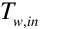 = Entering water temperature, K
= Entering water temperature, K
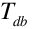 = Entering air dry-bulb temperature, K
= Entering air dry-bulb temperature, K
 = Entering air wet-bulb temperature, K
= Entering air wet-bulb temperature, K
 = Load side air volumetric flow rate, m3/s
= Load side air volumetric flow rate, m3/s
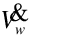 = Source side water volumetric flow rate, m3/s
= Source side water volumetric flow rate, m3/s
 = Total cooling capacity, W
= Total cooling capacity, W
 = Sensible cooling capacity, W
= Sensible cooling capacity, W
 = Power consumption (cooling mode), W
= Power consumption (cooling mode), W
 = Source side heat transfer rate (cooling mode), W
= Source side heat transfer rate (cooling mode), W
 = Total heating capacity, W
= Total heating capacity, W
 = Power consumption (heating mode), W
= Power consumption (heating mode), W
 = Source side heat transfer rate (heating mode), W
= Source side heat transfer rate (heating mode), W
The inlet conditions or variables are divided by the reference conditions. This formulation allows the coefficients to fall into smaller range of values. Moreover, the value of the coefficient indirectly represents the sensitivity of the output to that particular inlet variable. The reference conditions used when generating the performance coefficients must be the same as the reference conditions used later in the model. The reference temperature  is fixed at 283K. Temperature unit of Kelvin is used instead of Celsius to keep the ratio of the water inlet temperature and reference temperature positive should the water inlet temperature drop below the freezing point.
is fixed at 283K. Temperature unit of Kelvin is used instead of Celsius to keep the ratio of the water inlet temperature and reference temperature positive should the water inlet temperature drop below the freezing point.
For cooling mode, the reference conditions; reference load side air volumetric flow rate  ,reference source side water volumetric flow rate
,reference source side water volumetric flow rate ,reference sensible capacity
,reference sensible capacity  and reference power input
and reference power input 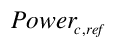 are the conditions when the heat pump is operating at the highest cooling capacity or reference cooling capacity
are the conditions when the heat pump is operating at the highest cooling capacity or reference cooling capacity indicated in the manufacturer’s catalog. Note that the reference conditions for heating mode might differ from the reference conditions specified for the cooling mode.
indicated in the manufacturer’s catalog. Note that the reference conditions for heating mode might differ from the reference conditions specified for the cooling mode.
Coefficient estimation procedure:[LINK]
The generalized least square method is used to generate the coefficients. This method utilizes an optimization method which calculates the coefficients that will give the least amount of differences between the model outputs and the catalog data. A set of coefficients for the cooling mode is generated which includes A1-A5 for total cooling capacity, B1-B6 for sensible cooling capacity, and C1-C5 for power consumption. The same procedure is repeated for the heating mode to generate the coefficients E1-E5 (total heating capacity) and F1-F5 (power consumption). An information flow chart showing the inputs, reference conditions, performance coefficients and outputs are shown in the figure below:
Zone Air DX Dehumidifier[LINK]
This model, object name ZoneHVAC:Dehumidifier:DX, simulates the thermal performance and electric power consumption of conventional mechanical dehumidifiers. These systems use a direct expansion (DX) cooling coil to cool and dehumidify an airstream. Heat from the DX system’s condenser section is rejected into the cooled/dehumidified airstream, resulting in warm dry air being supplied from the unit. In EnergyPlus, this object is modeled as a type of zone equipment (ref. ZoneHVAC:EquipmentList and ZoneHVAC:EquipmentConnections).
The model assumes that this equipment dehumidifies and heats the air. If used in tandem with another system that cools and dehumidifies the zone air, then the zone dehumidifier should be specified as the lowest cooling priority in the ZoneHVAC:EquipmentList object for best control of zone temperature and humidity levels. With this zone equipment prioritization, the other cooling and dehumidification system would operate first to meet the temperature setpoint (and possibly meet the high humidity setpoint as well). If additional dehumidification is needed, then the zone dehumidifier would operate. The sensible heat generated by the dehumidifier is carried over to the zone air heat balance for the next HVAC time step.
Model Description[LINK]
The user must input water removal, energy factor and air flow rate at rated conditions (26.7°C, 60% RH). Three performance curves must also be specified to characterize the change in water removal and energy consumption at part-load conditions:
- Water removal curve (function of inlet air temperature and relative humidity)
- Energy factor curve (function of inlet air temperature and relative humidity)
- Part load fraction correlation (function of part load ratio)
- The water removal modifier curve is a biquadratic curve with two independent variables: dry-bulb temperature and relative humidity of the air entering the dehumidifier. The output of this curve is multiplied by the Rated Water Removal to give the water removal rate at the specific entering air conditions at which the dehumidifier is operating (i.e., at temperature/relative humidity different from the rating point conditions). If the output of this curve is negative, then a warning message is issued and it is reset to 0.0.
where
Tin = dry-bulb temperature of the air entering the dehumidifier, °C
RHin = relative of the air entering the dehumidifier, % (0-100)
- The energy factor modifier curve is a biquadratic curve with two independent variables: dry-bulb temperature and relative humidity of the air entering the dehumidifier. The output of this curve is multiplied by the Rated Energy Factor to give the energy factor at the specific entering air conditions at which the dehumidifier is operating (i.e., at temperature/relative humidity different from the rating point conditions). If the output of this curve is negative, then a warning message is issued and it is reset to 0.0.
- The part load fraction (PLF) correlation curve is a quadratic or a cubic curve with the independent variable being part load ratio (PLR = water removal load to be met / dehumidifier steady-state water removal rate). The part load ratio is divided by the output of this curve to determine the dehumidifier runtime fraction. The part load fraction correlation accounts for efficiency losses due to compressor cycling.
or
where
The part load fraction correlation should be normalized to a value of 1.0 when the part load ratio equals 1.0 (i.e., no efficiency losses when the dehumidifier runs continuously for the simulation timestep). For PLR values between 0 and 1 (0 <= PLR < 1), the following rules apply:
0.7 <= PLF <= 1.0 and PLF >= PLR
If PLF < 0.7 a warning message is issued, the program resets the PLF value to 0.7, and the simulation proceeds. The runtime fraction of the dehumidifier is defined as PLR/PLF. If PLF < PLR, then a warning message is issued and the runtime fraction of the dehumidifier is set to 1.0.
Mechanical dehumidifier typically have long runtimes with minimal compressor cycling. So, a typical part load fraction correlation might be:
PLF = 0.95 + 0.05(PLR)
If the user wishes to model no efficiency degradation due to compressor cycling, the part load fraction correlation should be defined as follows:
PLF = 1.0 + 0.0(PLR)
All three part-load curves are accessed through EnergyPlus’ built-in performance curve equation manager (Curve:Quadratic, Curve:Cubic and Curve:Biquadratic). It is not imperative that the user utilize all coefficients shown in curve equations above if their performance equation has fewer terms (e.g., if the user’s PartLoadFrac performance curve is linear instead of quadratic, simply enter the values for a and b, and set coefficient c equal to zero).
For any simulation time step when there is a water removal load to be met, the dehumidifier is available to operate (via availability schedule), and the inlet air dry-bulb temperature is within the minimum and maximum dry-bulb temperature limits specified in the input file for this object, the water removal rate for the dehumidifier is calculated as follows:
where
 = dehumidifier steady-state water removal rate, kg/s
= dehumidifier steady-state water removal rate, kg/s
 = density of water, kg/m3
= density of water, kg/m3
 = rated water removal rate (user input), L/day
= rated water removal rate (user input), L/day
The Zone Dehumidifier Part-Load Ratio (output variable) is then calculated, with the result constrained to be from 0.0 to 1.0:
The steady-state and average electrical power consumed by the dehumidifier are calculated next using the following equations:
where
 = dehumidifier steady-state electric power, W
= dehumidifier steady-state electric power, W
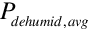 = Zone Dehumidifier Electric Power, W (output variable)
= Zone Dehumidifier Electric Power, W (output variable)
 = rated energy factor (user input), L/kWh
= rated energy factor (user input), L/kWh
 = off-cycle parasitic electric load (user input), W
= off-cycle parasitic electric load (user input), W
If the dehumidifier is unavailable to operate for the time period (via the specified availability schedule) then Zone Dehumidifier Electric Power is set equal to zero.
The average water removal rate (kg/s) for the simulation time step is then calculated:
The Zone Dehumidifier Sensible Heating Rate (output variable) is calculated as follows:
where
hfg = enthalpy of vaporization of air, J/kg
The Zone Dehumidifier Sensible Heating Rate (W) is calculated during each HVAC simulation time step, and the results are averaged for the timestep being reported. However, this sensible heating is carried over to the zone air heat balance for the next HVAC time step (i.e., it is reported as an output variable for the current simulation time step but actually impacts the zone air heat balance on the following HVAC time step).
The air mass flow rate through the dehumidifier is determined using the Rated Air Flow Rate (m3/s) entered in the input, PLR, and converting to mass using the density of air at rated conditions (26.7C, 60% RH) and local barometric pressure accounting for altitude
p=101325*(1-2.25577E-05*Z)**5.2559 where p=pressure in Pa and Z=altitude in m:
where
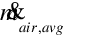 = average air mass flow rate through dehumidifier, kg/s
= average air mass flow rate through dehumidifier, kg/s
 = rated air flow rate (user input), m3/s
= rated air flow rate (user input), m3/s
 = density of air at 26.7°C , 60% RH and local barometric pressure, kg/m3
= density of air at 26.7°C , 60% RH and local barometric pressure, kg/m3
The dry-bulb temperature and humidity ratio of the air leaving the dehumidifier are calculated as follows:
where
Tout =Zone Dehumidifier Outlet Air Temperature, C (output variable). Represents the
outlet air temperature when the dehumidifier is operating.
Tin = inlet air dry-bulb temperature, C
 = heat capacity of air, J/kg
= heat capacity of air, J/kg
win = inlet air humidity ratio, kg/kg
wout = outlet air humidity ratio, kg/kg
If the dehumidifier does not operate for a given HVAC simulation time step, then the outlet air dry-bulb temperature and humidity ratio are set equal to the corresponding inlet air values.
Since the sensible heating rate impacts the zone air heat balance on the following HVAC time step and is passed to the heat balance via an internal variable, the dry-bulb temperature of the dehumidifier’s HVAC outlet air node (System Node Temperature) will always be set equal to the dehumidifier’s HVAC inlet air node temperature. Therefore, when the dehumidifier operates the Zone Dehumidifier Outlet Air Temperature (output variable) will not be equal to the System Node Temperature for the dehumidifier’s HVAC outlet node.
Finally, the following additional output variables are calculated:
where
Qsensible~~= output variable ‘Zone Dehumidifier Sensible Heating Energy [J]’
Edehumid = output variable ‘Zone Dehumidifier Electric Energy [J]’
Poff-cycle,avg = output variable ‘Zone Dehumidifier Off Cycle Parasitic Electric Power [W]’
Eoff-cycle = output variable ‘Zone Dehumidifier Off Cycle Parasitic Electric Energy [J]’
mwater~~= output variable ‘Zone Dehumidifier Removed Water Mass [kg]’
 ~~= output variable ‘Zone Dehumidifier Condensate Volume Flow Rate [m3/s]’
~~= output variable ‘Zone Dehumidifier Condensate Volume Flow Rate [m3/s]’
 = output variable ‘Zone Dehumidifier Condensate Volume [m3]’
= output variable ‘Zone Dehumidifier Condensate Volume [m3]’
Energy Recovery Ventilator[LINK]
The input object ZoneHVAC:EnergyRecoveryVentilator provides a model for a stand alone energy recovery ventilator (ERV) that is a single-zone HVAC component used for exhaust air heat recovery (see figure below). This compound object consists of three required components: a generic air-to-air heat exchanger (see object HeatExchanger:AirToAir:SensibleAndLatent), a supply air fan, and an exhaust air fan (see object Fan:OnOff). An optional controller (see object ZoneHVAC:EnergyRecoveryVentilator:Controller) may be used to simulate economizer (free cooling) operation.
This compound object models the basic operation of supply and exhaust air fans and an air-to-air heat exchanger. The stand alone ERV operates whenever the unit is scheduled to be available (Availability schedule). The stand alone ERV object can be used in conjunction with an economizer feature whereby heat exchange is suspended whenever free cooling is available (i.e., air flow is fully bypassed around a fixed-plate heat exchanger or the rotation of a rotary heat exchanger is stopped).
To model a stand alone ERV connected to a single zone, the input data file should include the following objects:
Model Description[LINK]
The purpose of this compound component is to simply call the individual component models and optional controller for each energy recovery ventilator. Since this equipment is not associated with an air loop, the compound object sets the supply and exhaust air mass flow rates through the ventilator. This compound object is also used to report the total, sensible and latent energy supplied to the zone, as well as the total electrical energy consumed by all of the individual components (supply air fan, exhaust air fan and heat exchanger parasitics).
During each similation time step, the air mass flow rate at the supply air and exhaust air inlets is set based on the stand alone ERV’s availablility schedule and the specified volumetric air flow rates as follows:
IF (availability schedule value > 0) THEN
ELSE
where:
 = mass flow rate of the supply air stream, kg/s
= mass flow rate of the supply air stream, kg/s
 = mass flow rate of the exhaust air stream, kg/s
= mass flow rate of the exhaust air stream, kg/s
 = density of dry air at local barometric pressure (adjusted for altitude) and 20 ºC, kg/m3
= density of dry air at local barometric pressure (adjusted for altitude) and 20 ºC, kg/m3
 = volumetric flow rate of the supply air stream, m3/s
= volumetric flow rate of the supply air stream, m3/s
 = volumetric flow rate of the exhaust air stream, m3/s
= volumetric flow rate of the exhaust air stream, m3/s
With the supply and exhaust inlet air mass flow rates set, the compound object then calls the generic air-to-air heat exchanger model to determine its supply air and exhaust air exiting conditions based on the inputs specified in the heat exchanger object. The supply air and exhaust air fans are then modeled to determine the final conditions of the air streams exiting the stand alone energy recovery ventilator. The heat exchanger and fan models are described in detail elsewhere in this document (reference: HeatExchanger:AirToAir:SensibleAndLatent and Fan:OnOff).
The sensible heat transfer rate to the zone by the stand alone ventilator is then calculated as follows:
where:
 = sensible energy transfer rate to the zone, W
= sensible energy transfer rate to the zone, W
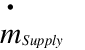 = mass flow rate of the supply air stream, kg/s
= mass flow rate of the supply air stream, kg/s
hSupplyOutlet = enthalpy of the air being supplied to the zone, J/kg
hExhaustInlet~~= enthalpy of the air being exhausted from the zone through the ventilator, J/kg
HRmin = enthalpies evaluated at a constant humidity ratio, the minimum humidity ratio
of the supply air outlet or the exhaust air inlet
The resulting sensible energy transfer rate is passed to the zone equipment manager and added to the zone load to be met by other heating or cooling equipment. Since the stand alone ERV is intended to reduce the outdoor air load through heat exchange and not meet that load completely, the stand alone heat exchanger must be modeled first in the list of zone equipment. This is accomplished by setting the stand alone ERV priority for cooling and heating higher than that of other zone cooling or heating equipment (reference: ZoneHVAC:EquipmentList).
When economizer (free cooling) operation is desired, a controller is coupled to the stand alone ERV by providing the name of the controller object in the ERV controller input field. This controller determines when the air-side economizer is active (i.e., air flow is fully bypassed around a fixed-plate heat exchanger or the rotation of a rotary heat exchanger is stopped) based on the controller inputs (Ref. ZoneHVAC:EnergyRecoveryVentilator:Controller).
At the end of each HVAC simulation time step, this compound object reports the heating or cooling rate and energy delivered to the zone, as well as the electric power and consumption by the ventilator. In terms of thermal energy delivered to the zone, the sensible, latent and total energy transfer rate to the zone is calculated as follows:
where:
 = total energy transfer rate to the zone, W
= total energy transfer rate to the zone, W
 = sensible energy transfer rate to the zone, W
= sensible energy transfer rate to the zone, W
 = latent energy transfer rate to the zone, W
= latent energy transfer rate to the zone, W
 = mass flow rate of the supply air stream, kg/s
= mass flow rate of the supply air stream, kg/s
hSupplyOutlet = enthalpy of the air being supplied to the zone, J/kg
hExhaustInlet~~= enthalpy of the air being exhausted from the zone through the ventilator, J/kg
HRmin = enthalpies evaluated at a constant humidity ratio, the minimum humidity ratio
of the supply air outlet or the exhaust air inlet
Since each of these energy transfer rates can be calculated as positive or negative values, individual reporting variables are established for cooling and heating and only positive values are reported. The following calculations are representative of what is done for each of the energy transfer rates:
IF ( < 0.0 ) THEN
< 0.0 ) THEN
 = ABS (
= ABS ( )
)
 ~~ = 0.0
~~ = 0.0
ELSE
 ~~ = 0.0
~~ = 0.0
 ~~ =
~~ = 
where:
 = output variable ‘Zone Ventilator Total Cooling Rate, W’
= output variable ‘Zone Ventilator Total Cooling Rate, W’
 = output variable ‘Zone Ventilator Total Heating Rate, W’
= output variable ‘Zone Ventilator Total Heating Rate, W’
In addition to heating and cooling rates, the heating and cooling energy supplied to the zone is also calculated for the time step being reported. The following example for total cooling energy is representative of what is done for the sensible and latent energy as well as the heating counterparts.
where:
 = output variable ‘Zone Ventilator Total Cooling Energy, J’
= output variable ‘Zone Ventilator Total Cooling Energy, J’
TimeStepSys = HVAC system simulation time step, hr
(Note: Some of this information also appears in the Input Output Reference for EnergyPlus. It is repeated here for clarity.)
The input object ZoneHVAC:UnitHeater provides a model for unit heaters that are zone equipment units which are assembled from other components and are a simplification of unit ventilators. They contain only a fan and a heating coil. These components are described elsewhere in this document. The unit heater input simply requires the names of these components, which have to be described elsewhere in the input. The input also requires the name of an availability schedule, maximum airflow rate, and maximum and minimum hot water volumetric flow rates. The unit is connected to the zone inlet and exhaust nodes by specifying unit inlet and outlet node names. Note that the unit air inlet node should be the same as a zone exhaust node and the unit outlet node should be the same as a zone inlet node.
While the control of the heating coil is similar to the fan coil units and the unit ventilator, the overall control of the unit heater is much different. There are four different modes in which a unit heat can operate based on the user input:
OFF: In this mode, the unit has been scheduled off. All flow rates are set to zero, and the temperatures are set to zone conditions.
NO LOAD OR COOLING/ON-OFF FAN CONTROL: In this mode, the unit is available, but there is no heating load. With On-Off fan control, the fan will only run when there is a heating load. Since there is no heating load in this mode, all flow rates are set to zero, and the temperatures are set to zone conditions. Since the unit heater is designed only to provide heating, the presence of a cooling load signifies that the unit should not be running.
NO LOAD OR COOLING/CONTINUOUS FAN CONTROL: In this mode, the unit is available and the fan is controlled to be running continuously. If it is scheduled to be available, the fan runs and circulates air to the space. While no direct heating is provided, any heat added by the fan is introduced into the space with the circulation of the air. If the fan is scheduled off, the fan will not run (this is identical to on-off control with no load).
HEATING: In this mode, the unit and fan are on/available, and there is a heating load. The heating coil is modulated (constant fan speed) to meet the heating load. Control of the heating coil and its flow rate is identical to the fan coil unit and unit ventilator. The flow rate of air through the unit is controlled by the user input and schedules.
Unit Ventilator[LINK]
(Note: Some of this information also appears in the Input Output Reference for EnergyPlus. It is repeated here for clarity.)
The input object ZoneHVAC:UnitVentilator provides a model for unit ventilators that are zone equipment units which are assembled from other components. They contain a built-in outdoor air mixer, a fan, a heating coil, and a cooling coil. These components are described elsewhere in this document, except the built-in outdoor air mixer which is contained within the unit ventilator statement. The unit ventilator input simply requires the names of these other three components, which have to be described elsewhere in the input. The input also requires the name of an availability schedule, maximum airflow rate, outdoor air control information (control type and schedules), an outdoor airflow rate, and maximum and minimum hot and cold water mass flow rates. The unit is connected to the zone inlet and exhaust nodes and the outdoor air by specifying unit inlet, outlet, outdoor air and exhaust (relief) air node names. Note that the unit air inlet node should be the same as a zone exhaust node and the unit outlet node should be the same as a zone inlet node. In general, the unit ventilator input is very similar to the fan coil unit input, and the unit is connected to a hot water loop (demand side) through its hot water coil and to a chilled water loop (demand side) through its cooling coil.
Controls and Outdoor Air[LINK]
The main difference between the fan coil and unit ventilator input is that the unit ventilator has a built-in outdoor air mixer with its own specialized controls. The outdoor air control type can be selected from one of the following options: “variable percent”, “fixed temperature” or “fixed amount”. In fixed temperature control, the amount of outdoor air is varied between the minimum outdoor air fraction (specified by a schedule) and 100% outdoor air to obtain a mixed air temperature as close as possible to the temperature schedule defined in the input. Variable percent control will also vary the amount of outdoor air between the minimum and maximum fractions (both specified in input by the user) to meet the load without the use of a coil if possible. In fixed amount control, the outdoor air flow rate is fixed to the specified value by the user. In this control strategy, the maximum outdoor air flow rate and schedule are automatically set to be equal to the minimum outdoor air flow rate and schedule. These control types are based on the 2004 ASHRAE Systems and Equipment Handbook (pp. 31.1-31.3) description of unit ventilator systems.
The unit is controlled to meet the zone (remaining) heating or cooling demand. If there is a heating demand, the cooling coil is off and the hot water flow through the heating coil is throttled to meet the demand. The hot water control node must be specified (same as the hot water coil inlet node) as well as maximum and minimum possible hot water volumetric flow rates. If there is a cooling demand from the zone, the hot water coil is off and the chilled water flow through the cooling coil is throttled to meet the load. The cooling coil control node must be specified (same as the cooling coil inlet node) and the maximum and minimum chilled water volumetric flow rates must be given. Finally both heating and cooling require a convergence tolerance, which is the tolerance denoting how closely the fan coil unit will meet the heating or cooling load. The tolerance is always relative to the zone load.
Overall, control of the unit must consider the outdoor air. Here is a more detailed description of the overall unit control:
OFF: Unit is schedule off or there is no load on it. All flow rates are set to zero and the temperatures are set to zone conditions (except for the outdoor air inlet). Outdoor air requirements will not override this condition.
HEATING/NO COIL/VARIABLE PERCENT: The unit is on, there is a heating load, no heating coil is present or it has been scheduled off, and variable percent outdoor air control type has been specified. In this case, the variable percent outdoor air controls what happens with the outdoor air. If the outside temperature is greater than the return temperature, then the outdoor air is set to the maximum as defined by the user input. If the outdoor air temperature is less than the return temperature from the zone, then the outdoor air is set to the minimum outdoor air flow rate as defined by the user. Since a coil is not present to further condition the supply air, the zone simply receives whatever temperature air results from the outdoor air controls.
HEATING/NO COIL/FIXED TEMPERATURE: The unit is on, there is a heating load, no heating coil is present or it has been scheduled off, and fixed temperature has been specified. The unit ventilator tries to use outdoor air as best as possible to meet the temperature goal. If it cannot meet this goal because the temperature goal is not between the zone return temperature and the outdoor air temperature, then the unit ventilator will either use the maximum or minimum outdoor air flow rate.
HEATING/NO COIL/FIXED AMOUNT: The unit is on, there is a heating load, no heating coil is present or it has been scheduled off, and fixed amount control has been specified. The unit ventilator fixes the outdoor air flow rate as defined by the user and sets the maximum and minimum outdoor air flow rate to be equal in order to avoid the variation of outdoor air flow rate between the maximum and minimum values. Since a coil is not present to further condition the supply air, the zone simply receives whatever temperature air results from the outdoor air controls.
HEATING/WITH COIL/VARIABLE PERCENT: The unit is on, there is a heating load, and variable percent control is specified. The outdoor air fraction is set to the minimum outdoor air fraction (schedule based), and the heating coil is activated. The heating coil attempts to meet the remaining load on the zone being served by the unit ventilator.
HEATING/WITH COIL/FIXED AMOUNT: The unit is on, there is a heating load, a heating coil is present and is scheduled on, and fixed amount control has been specified. The unit ventilator fixes the outdoor air flow rate as defined by the user and sets the maximum and minimum outdoor air flow rate to be equal in order to avoid the variation of outdoor air flow rate between the maximum and minimum values. The heating coil then attempts to meet any remaining zone heating load.
COOLING/NO COIL/VARIABLE PERCENT: The unit is on, there is a cooling load, no coil is present or it has been scheduled off, and variable percent outdoor air control type has been specified. In this case, the variable percent outdoor air controls what happens with the outdoor air. If the outside temperature is greater than the return temperature, then the outdoor air is set to the minimum as defined by the user input. If the outdoor air temperature is less than the return temperature from the zone, then the outdoor air is set to the maximum outdoor air flow rate as defined by the user. This may be somewhat simplistic in that it could result in overcooling of the space. However, since a temperature goal was not established, this is the best that can be done by the simulation. Since a coil is not present to further condition the supply air, the zone simply receives whatever temperature air results from the outdoor air controls.
COOLING/NO COIL/FIXED TEMPERATURE: The unit is on, there is a cooling load, no cooling coil is present or it has been scheduled off, and fixed temperature has been specified. The unit ventilator tries to use outdoor air as best as possible to meet the temperature goal. If it cannot meet this goal because the temperature goal is not between the zone return temperature and the outdoor air temperature, then the unit ventilator will either use the maximum or minimum outdoor air flow rate in the same fashion as the variable percent outdoor air control.
COOLING/NO COIL/FIXED AMOUNT: The unit is on, there is a cooling load, no cooling coil is present or it has been scheduled off, and fixed amount control has been specified. The unit ventilator fixes the outdoor air flow rate as defined by the user and sets the maximum and minimum outdoor air flow rate to be equal in order to avoid the variation of outdoor air flow rate between the maximum and minimum values. Since a coil is not present to further condition the supply air, the zone simply receives whatever temperature air results from the outdoor air controls.
COOLING/WITH COIL/VARIABLE PERCENT: The unit is on, there is a cooling load, a coil is present and is scheduled on, and variable percent outdoor air control type has been specified. In this case, the percentage of outdoor air is set to the minimum flow outdoor air flow rate. The coil then attempts to meet any remaining zone load.
COOLING/WITH COIL/FIXED TEMPERATURE: The unit is on, there is a cooling load, a cooling coil is present and is scheduled on, and fixed temperature has been specified. The unit ventilator tries to use outdoor air as best as possible to meet the temperature goal. If it cannot meet this goal because the temperature goal is not between the zone return temperature and the outdoor air temperature, then the unit ventilator will either use the maximum or minimum outdoor air flow rate in the same fashion as the fixed temperature outdoor air control for the “no coil” conditions. The cooling coil then attempts to meet any remaining zone load.
COOLING/WITH COIL/FIXED AMOUNT: The unit is on, there is a cooling load, a cooling coil is present and is scheduled on, and fixed amount control has been specified. The unit ventilator fixes the outdoor air flow rate as defined by the user and sets the maximum and minimum outdoor air flow rate to be equal in order to avoid the variation of outdoor air flow rate between the maximum and minimum values. The cooling coil then attempts to meet any remaining zone cooling load.
Note: the unit ventilator controls are strictly temperature based and do not factor humidity into the equation (not an enthalpy economy cycle but rather a simple return air economy cycle). In addition, temperature predictions are not strict energy balances here in the control routine though in the mixing routine an energy balance is preserved.
Variable Refrigerant Flow Terminal Unit[LINK]
Variable refrigerant flow zone terminal units are used exclusively with variable refrigerant flow (VRF) air conditioning systems (ref: AirConditioner:VariableRefrigerantFlow and ZoneTerminalUnitList). The terminal units operate to satisfy a heating or cooling load in a zone based on a zone thermostat temperature set point. A direct-expansion (DX) cooling and/or DX heating coil is specified depending on the operating mode required. Outdoor ventilation air is modeled with the use of an outside air mixer object. Outside air may be provided to the zone only when the coil is operating or can be supplied continuously even when the coil is not operating. A supply air fan is also required and can be modeled as either draw through as shown in the figure below or as blow through where the fan inlet node would be connected to the outside air mixer mixed air node. If an outside air mixer is not used, the fan inlet node would be connected to the zone exhaust node.
As described previously, the terminal units operate to satisfy a heating or cooling load in a zone based on a zone thermostat temperature set point (Zone Control:Thermostatic). Each simulation time step, EnergyPlus performs a zone air heat balance to determine if cooling or heating is required to meet the zone thermostat set points, excluding any impacts from zone terminal unit operation.
Terminal unit performance is then modeled with all heating/cooling coils off but the supply air fan operates as specified by the user. If the zone air heat balance plus the impact of terminal unit operation with coils off results in no requirement for heating or cooling by the terminal unit coils, or if the terminal unit is scheduled off (via its availability schedule), then the terminal unit coils do not operate and the terminal unit’s part-load ratio output variable is set to 0. If the model determines that cooling or heating is required and the terminal unit is scheduled to operate, the model calculates the part-load ratio of the cooling and heating coils in order to meet the thermostat set point temperature.
The following sections describe the performance calculations for cooling-mode and heating-mode.
Model Description[LINK]
Zone terminal units meet a zone load as determined by a zone thermostat. The DX coils within a zone terminal unit will operate to meet a sensible zone load and all terminal units are controlled to either meet a zone sensible cooling load or a zone sensible heating load. This model does not provide for simultaneous cooling and heating.
Given a zone load, the model calculates the part-load ratio of the terminal unit such that the terminal unit’s “net” sensible capacity is equal to the zone load (if sufficient capacity is available). If it is determined that the part-load ratio of the zone terminal unit will be equal to 1, the DX cooling coil’s capacity is calculated in the same manner as described for single-speed DX cooling coils (ref: Coil:Cooling:DX:SingleSpeed). When it is determined that the part-load ratio of the zone terminal unit will be less than 1, the DX cooling coil’s capacity will be modulated through a reduction in refrigerant flow rate and an iterative solution technique will be used to calculate the performance of the DX cooling coil. For DX heating coils, capacity is calculated in the same manner as described for single-speed DX heating coils (ref: Coil:Heating:DX:SingleSpeed).
The “net” sensible full load cooling capacity is then compared to the zone sensible load. If the “net” sensible full load capacity is less than or equal to the absolute value of the zone sensible load, the DX coil operates at the maximum available capacity and, as a result, the zone air heat balance adjusts the zone air temperature. If the “net” sensible full load capacity is greater than the absolute value of the zone sensible load, an iterative solution technique is used to determine the total capacity required to meet the zone sensible load. This iteration loop entails successive modeling of DX coil performance and the loop iterates on the required total capacity until the operating “net” sensible capacity is equal to the zone sensible load.
Average Air Flow Calculations[LINK]
The variable refrigerant flow (VRF) terminal unit operates based on user-specified (or autosized) air flow rates. The VRF terminal unit’s supply air flow rate during cooling operation may be different than the supply air flow rate during heating operation. In addition, the supply air flow rate when no cooling or heating is required but the supply air fan remains ON can be different than the air flow rates when cooling or heating is required. The outside air flow rates can likewise be different in these various operating modes. The model takes these different flow rates into account when modeling the terminal unit, and the average air flow rate for each simulation time step is reported on the inlet/outlet air nodes of the various VRF terminal unit components in proportion to the calculated cycling ratio of the heat pump condenser. If the compressor does not cycle for a specific simulation time step then the heating or cooling air flow rate as specified by the user is assumed for the entire time step.
The average supply air and outdoor air mass flow rates through the terminal unit for the HVAC simulation time step are calculated based on the cycling ratio of the heat pump condenser as follows:
where:
 = average supply air mass flow rate during the time step, kg/s
= average supply air mass flow rate during the time step, kg/s
 = supply air mass flow rate when the coil is ON, kg/s
= supply air mass flow rate when the coil is ON, kg/s
CyclingRatio = cycling ratio of the heat pump condenser (heating or cooling)
 = supply air mass flow rate when the coil is OFF, kg/s
= supply air mass flow rate when the coil is OFF, kg/s
 = average outside air mass flow rate during the time step, kg/s
= average outside air mass flow rate during the time step, kg/s
 = average outside air mass flow rate when the coil is ON, kg/s
= average outside air mass flow rate when the coil is ON, kg/s
 = average outside air mass flow rate when the coil is OFF, kg/s
= average outside air mass flow rate when the coil is OFF, kg/s
The supply air and outside air flow rates when the DX cooling coil or the DX heating coil is ON are specified by the user (i.e., supply air volumetric flow rate during cooling operation, supply air volumetric flow rate during heating operation, outside air volumetric air flow rate during cooling operation, and outside air volumetric air flow rate during heating operation) and are converted from volumetric to mass flow rate. If the user has specified cycling fan/cycling coil operation (i.e. supply air fan operating mode schedule value is equal to 0), then the supply air and outside air mass flow rates when the coil is OFF are zero. If the user has specified constant fan/cycling coil operation (i.e. supply air fan operating mode schedule value is greater than 0), then the user-defined air flow rates when no cooling or heating is needed are used when the coil is OFF.
There is one special case. If the supply air fan operating mode schedule value specifies constant fan operation and the user also specifies that the supply air volumetric flow rate when no cooling or heating is needed is zero (or field is left blank), then the model assumes that the supply air and outside air mass flow rates when the coil is OFF are equal to the corresponding air mass flow rates when the cooling or heating coil was last operating (ON).
Calculation of Outlet Air Conditions[LINK]
When the supply air fan cycles on and off with the terminal unit coils (AUTO fan), the calculated outlet air conditions (temperature, humidity ratio, and enthalpy) from the DX heating coil or the DX cooling coil at full-load (steady-state) operation are reported on the appropriate coil outlet air node. The air mass flow rate reported on the air nodes is the average air mass flow rate proportional to the cycling ratio of the coil (see Average Air Flow Calculations above).
When the supply air fan operates continuously while the terminal unit coils cycle on and off (fan ON), the air mass flow rate reported on the air nodes is the average air mass flow rate proportional to the cycling ratio of the coil (see Average Air Flow Calculations above). Since the air flow rate can be different when the coil is ON compared to when the coil is OFF, then the average outlet air conditions from the DX heating coil or the DX cooling coil are reported on the appropriate coil outlet air node.
Calculation of Zone Heating and Cooling Rates[LINK]
At the end of each HVAC simulation time step, this compound object reports the heating or cooling rate and energy delivered to the zone. In terms of thermal energy delivered to the zone, the sensible, latent and total energy transfer rate to the zone is calculated as follows:
where:
 = total energy transfer rate to the zone, W
= total energy transfer rate to the zone, W
 = sensible energy transfer rate to the zone, W
= sensible energy transfer rate to the zone, W
 = latent energy transfer rate to the zone, W
= latent energy transfer rate to the zone, W
 = average mass flow rate of the supply air stream, kg/s
= average mass flow rate of the supply air stream, kg/s
hout,avg = enthalpy of the air being supplied to the zone, J/kg
The terminal unit’s energy transfer rate is used by the program in the zone air heat balance to determine the final zone air conditions. If the terminal unit is capable of meeting the zone thermostat set point temperature, then these report variables are indicative of the zone loads and may be compared directly to the report variables for predicted zone loads (ref: Output:Variable, e.g., Zone Predicted Sensible Load to Setpoint Heat Transfer Rate).
Since each of these energy transfer rates can be calculated as positive or negative values, individual reporting variables are established for cooling and heating and only positive values are reported. The following calculations are representative of what is done for each of the energy transfer rates:
IF ( < 0.0 ) THEN
< 0.0 ) THEN
 = ABS (
= ABS ( )
)
 ~~ = 0.0
~~ = 0.0
ELSE
 ~~ = 0.0
~~ = 0.0
 ~~ =
~~ = 
ENDIF
where:
 = output variable ‘Zone VRF Air Terminal Total Cooling Rate, W’
= output variable ‘Zone VRF Air Terminal Total Cooling Rate, W’
 = output variable ‘Zone VRF Air Terminal Total Heating Rate, W’
= output variable ‘Zone VRF Air Terminal Total Heating Rate, W’
In addition to heating and cooling rates, the heating and cooling energy supplied to the zone is also calculated for the time step being reported. The following example for total zone cooling energy is representative of what is done for the sensible and latent energy as well as the heating counterparts.
where:
 = output variable ‘Zone VRF Air Terminal Total Cooling Energy, J’
= output variable ‘Zone VRF Air Terminal Total Cooling Energy, J’
TimeStepSys = HVAC system simulation time step, hr
Ventilated Slab[LINK]
Model Overview[LINK]
The input object ZoneHVAC:VentilatedSlab provides a model for ventilated slab systems that in general use outdoor air to “precool” slabs with colder nighttime air. This method of precooling the thermal mass of a space can be very effective when nighttime temperatures are low and the mass of the system is high enough to provide a significant amount of cooling potential during the day to counteract internal heat gains within a zone. Nearly all ventilated slabs are simple systems such as that shown in the right side of Figure 299. The fan is shown in a blow through position, but the model will allow either a blow or draw through configuration.
It should be noted that in Figure 299 the use of “unit ventilator” and “low temperature radiant system” do not imply that the user must also specify these elements in the input file. The ventilated slab model combines aspects of these two existing EnergyPlus features into a single model that the user specifies through the input shown in the Input/Output Reference.
The ventilated slab system has been implemented in a fashion that is similar to the “unit ventilator” system in EnergyPlus. The unit ventilator is a system that allows the user to bring in outdoor air (ventilation) that may or may not be tempered with a heating or cooling coil as shown the left side of Figure 299. The air can be delivered to the slab only (Figure 300), to the slab then to the space(Figure 301), and to several slabs in different areas in series (Figure 302). The model essentially combines the functionality of the low temperature radiant system (using air as a transport medium rather than water) and the unit ventilator. In some cases, the system may not meet all the zone heating and cooling load because it is operated not by setpoint of the zone but control temperature range and coil outlet air temperature set by user input. **Note that no coils are shown in Figure 302 for diagram simplicity but the implementation of the system shown in Figure 302 includes coils as in Figure 300 and Figure 301.
Connections to the Heat Balances[LINK]
The ventilated slab systems shown in the above diagrams connect or will connect to the various EnergyPlus heat balance equations in a variety of ways. All of the systems send outside or conditioned air through a slab or building element. This portion of the system acts in a fashion that is identical to the low temperature radiant systems. These surfaces that have the air being blown through them will impact the zone and air heat balances through the normal surface heat balances that interact with this surface. The ventilated slab will participate in the surface heat balances by exchanging radiation with other surfaces in the zone and in the air heat balances via convection to the zone air. So, the ventilated slab is handled identically to the low temperature radiant systems with respect to the zone and air heat balances. This information is valid for all three of the systems shown in the figures above.
For more information on the impact on the zone and air heat balances by the ventilated slab system, please consult the low temperature radiant system documentation and the EnergyPlus code.
The Cool Tower (object ZoneCoolTower:Shower) is available for modeling a cooltower (which is sometimes referred to as s wind tower or a shower cooling tower) which is a component that is intended to model a passive downdraught evaporative cooling (PDEC) that is designed to capture the wind at the top of a tower and cool the outdoor air using water evaporation before delivering it to a space. The air flow in these systems is natural as the evaporation process increases the density of the air causing it to fall through the tower and into the space without the aid of a fan. A cooltower typically consists of a water spray or an evaporative pad, a shaft, and a water tank or reservoir. Wind catchers to improve the wind-driven performance at the top of the tower are optional. Water is pumped over an evaporative device by water pump which is the only component consumed power for this system. This water cools and humidifies incoming air and then the cool, dense air naturally falls down through shaft and leaves through large openings at the bottom of cooltowers.
The shower cooling tower shown in figure below is controlled by a schedule and the specification of maximum water flow rate and volume flow rate as well as minimum indoor temperature. The actual flow rate of water and air can be controlled as users specify the fractions of water loss and flow schedule. The required input fields include effective tower height and exit area to obtain the temperature and flow rate of the air exiting the tower. A schedule and rated power for the water pump are also required to determine the power consumed. The component typically has a stand-alone water system that is not added to the water consumption from mains. However, users are required to specify the water source through an optional field, the name of water supply storage tank, in case any water comes from a water main.
The cooltower model employing a model of the inertial shower cooling tower is intended to establish the actual mass flow rate of the air that leaves the cooltower and the evaporation rate consumed during the processes within the cooltower. Like infiltration, ventilation, and earth tubes, the air is assumed to be immediately mixed with the zone air. The determination of simultaneous heat and mass transfer that occurs during natural evaporative cooling in cooltower is complicated. Therefore, some assumptions have been made to obtain the conditions of the air and water. All cooltowers are executed at the start of each time step called by HVAC manager, and the conditions of air temperature and humidity ratio in the zone will be corrected with any other air that enters the zone.
All temperatures in the following descriptions are in degrees C, mass flow rates are in kg/s, and volume flow rates are in m3/s.
Model Description[LINK]
The user must input the required information according to the Input Output Reference Manual (ref: ZoneCoolTower:Shower). The cooltower model requires a unique identifying name, an availability schedule, and the name of the zone being served. The schedule name must refer to a valid schedule type (range 0-1) and contain values of fractional cooltower operation as well as water pump operation. For the determination of the exit temperature and actual air volume flow rate, four additional inputs are required: effective tower height, exit area, fraction of flow schedule, and fraction of water loss. These define the conditions of the exit air, obtaining the conditions of outdoor air from the weather data and thus allow EnergyPlus to correct both the temperature and humidity level in the zone. The power consumed by the water pump can be directly determined by the schedule and rated power that the user inputs. The component is also controlled by the specification of minimum indoor temperature, maximum volume flow rate, and maximum water flow rate. These allow the model to prevent overcooling the zone or overestimation of the air volume flow rate. In addition, the user must input a flow control type according to the information that the user is able to obtain.
Simulation and Control[LINK]
The cooltower model first determines the temperature and volume flow rate of the exit air. Both parameters can be directly determined in case of water flow schedule control when the water flow rate is known. With the outdoor temperatures obtained from weather data, the exit air temperature (Tout) can be directly determined as functions of outdoor dry bulb temperature (DB), outdoor wet bulb temperature (WB), effective tower height (H) and water flow rate (WF) in l/min by using following equation.
The volume flow rate of the exit air (Q) can also be directly obtained as functions of water flow rate and effective tower height from the following equation.
In case of that the calculated air volume flow rate is greater than maximum air volume flow rate in this control, which leads to overestimation of actual volume flow rate of the exit air, the calculated air volume flow rate is replaced with the maximum.
For the simulation of wind-driven flow control where the water flow rate is unknown, the model determines velocity of the outlet air (Vout) as functions of effective tower height and wind speed of outdoor air (WS) as
The air volume flow rate (Q) is then calculated by
where A is opening area at the bottom of cooltower.
Substituting the air flow rate to the previous equation for Q, water flow rate is obtained as
Once water flow rate is determined, the model checks the limit of water flow rate that the user inputs, so that the model prevents overestimation of actual volume flow rate of the exit air. If the calculated water flow rate is greater than the maximum water flow rate, the maximum will be chosen. The model also replaces the calculated air volume flow rate with the maximum volume flow rate from the user input when the calculated is greater than the maximum. Then, the model calculates the air volume flow rate and exit temperature using the previous equation for Q and Tout.
This cooltower model allows the user to specify water loss due to drift or blow down and the loss of air flow (example: a cooltower which delivers air to both the interior and exterior of the building). If the user inputs the fraction of water loss or flow schedule that means some amount of the air actually goes to outside, the fractional values will be applied to previously calculated ones so that the model calculates both actual water flow rate (WFactual) and air volume flow rate (Qactual) as follows:
The model then determines the exit humidity ratio ( ) from the relation of mass balances below.
) from the relation of mass balances below.
In this case, actual mass flow rate at the inlet and outlet of cooltower cannot be correctly calculated with limited information. Thus, the model estimates initial conditions of the air based on the outdoor temperatures, the calculated exit air temperature, enthalpy of outdoor air (Hin) and outdoor barometric pressure (P). Assuming no enthalpy changes and pressure drops between inlet air and the initialized air, the humidity ratio and mass flow of the initialized air can be obtained by using EnergyPlus psychrometric functions and the following equation.
where  and
and  are the humidity ratio and air density of the initialized air and
are the humidity ratio and air density of the initialized air and  is the humidity ratio of outdoor air.
is the humidity ratio of outdoor air.
Therefore, the humidity ratio of exit air,  , is
, is
Once the humidity ratio at the exit is determined, the model can obtain the actual density ( ), specific heat (
), specific heat ( ), and mass flow rate (
), and mass flow rate ( ) of the air leaving cooltower by using EnergyPlus psychrometric function and following equation.
) of the air leaving cooltower by using EnergyPlus psychrometric function and following equation.
Assuming that the water temperature equals to outdoor wet bulb temperature, the model eventually determines density of the water and evaporation rate as bellows.
The earth tube model (input object ZoneEarthtube) provides a simple earth tube model that uses a complex ground heat transfer model to establish the temperature of the soil at the depth of the earth tube. The following information defines the basis for the model including the assumptions and mathematical equations. It supplements the information for the ZoneEarthtube input object given in the Input/Output Reference for EnergyPlus.
Input Requirement
Pipe : Pipe radius(m), Pipe thickness(m), Pipe length(m)
- Distance between the pipe outer surface and undisturbed soil (m),
- Pipe thermal conductivity (W/m-C),
Air velocity inside pipe(m/s), Depth of the radial center of pipe below ground (m)
Soil : Soil density(kg/m3), Soil specific heat(J/kg°C),
- Soil thermal Conductivity(W/m°C), Absorption coefficient,
Fraction of evaporation rate
Assumption(s)
- Convection flow inside the pipe is hydrodynamically and thermally developed.
- Soil temperature in the pipe vicinity is uniform after the particular distance from the center of the pipe(thickness of the annulus), so that pipe surface temperature is uniform after the distance ‘r’ from the center of the pipe, where ‘r’is the pipe radius.
- The temperature profile in the pipe vicinity is not affected by the presence of the pipe, so that pipe surface temperature is uniform at axial direction.
- The soil surrounding the pipe has homogeneous thermal conductivity.
Pipe has uniform cross section area at axial direction.
Wind velocity (m/s), u, is the annual average value. This is calculated from EnergyPlus weather data by averaging individual wind velocity values of the whole year. The convective heat transfer coefficient at the soil surface (W/m2°C), hs, is function of wind speed u. According to McAdams(1954) hs can be approximated by the following correlation (Krarti, 1995).
In case of he and hr, they can be determined by the following equations.
with a = 103 Pa/°C.
Average air temperature (°C), Tma, is also calculated from EnergyPlus weather data by averaging individual air temperature values of the whole year.
The appropriate value of hemispherical emittance of the ground surface, ε, is 0.93~0.96. Radiation constant (W/m2), ΔR, depends on soil radiative properties, air relative humidity, and effective sky temperature. An appropriate value of ΔR according to Krarti (1995) is 63 W/m2.
The absorption coefficient, β, depends on the soil absorptance and shading condition. The coefficient β is approximately equal to one minus the soil surface albedo. Albedo depends on soil cover and moisture content. Albedo=0.1 corresponds to wet soils, albedo=0.2 to moderate soils, and albedo=0.3 to dry soils.
Average solar radiation (W/m2), Sm, is determined from EnergyPlus weather data by averaging individual global horizontal solar radiation values of the whole year.
The fraction of evaporation rate, f, also depends mainly on the soil cover and the soil moisture level. Based on the results reported by Penman, it is recommended to estimate the fraction f as follows. For bare soil, f is directly proportional to soil moisture content. For instance, f=1 corresponds to saturated soils, f=0.6~0.8 to wet soils, f=0.4~0.5 to moist soils, f=0.1~0.2 to arid soils. For dry soils, f = 0, since no evaporation occurs. For covered soils, the fraction f is obtained by multiplying 0.7 by the value of f for bare soil depending on the soil moisture content (Krarti, 1995).
Relative humidity, ra, is also calculated from EnergyPlus weather data by averaging individual relative humidity values of the whole year.
The soil thermal diffusivity (m2/s), αs, and conductivity (W/m°C), ks, varies with the density and moisture content. According to the 1991 ASHRAE Handbook of HVAC Applications (Table 4, pp. 11.4), the following values are recommended under different conditions.
| Heavy soil, saturated |
2.42 |
9.04 |
| Heavy soil, damp solid masonry |
1.30 |
6.45 |
| Heavy soil, dry |
0.865 |
5.16 |
| Light soil, damp |
- |
- |
| Light soil, dry |
0.346 |
2.80 |
Annual angular frequency, w, is equal to 1.992 x 10-7rad/s, and dampening depth (m), D, is calculated from the following equation:
The value of δ is evaluated as follows.
Amplitude of the air temperature (°C), Tva, can be evaluated from EnergyPlus weather data by dividing the difference between the maximum and minimum air temperature value of the whole year by two. Similarly, amplitude of the solar radiation (W/m2), Sv, can also be determined from weather data by dividing the difference between the maximum and minimum solar radiation value of the whole year by two.
Phase angle between the insolation and the air temperature (rad), φI , is calculated by subtracting insolation phase angle from air temperature phase angle. Phase angle of insolation and air temperature is the point from the beginning of the year at which the insolation and air temperature respectively reaches the minimum value among the whole year.
Phase constant of the air (sec), t0a, is the time elapsed from the beginning of the year at which the air temperature reaches the minimum value in the year.
By using all the input parameters and variables described above, average soil surface temperature (°C), Tm, amplitude of the soil surface temperature variation (°C), As, phase constant of the soil surface (sec), t0, and phase angle difference between the air and soil surface temperature (rad), Φs, can be evaluated as follows 1):
(Note: Tm, As, and t0 are calculated by the CalcSoilSurfTemp program and are inputs to EnergyPlus. The remainder of this section describes what has been implemented in EnergyPlus.)
The symbols || || and Arg denote the modulus and the argument of a complex number respectively. In order to calculate As and Φs, the complex number under consideration can be rearranged as the following form:
Assuming a homogeneous soil of constant thermal diffusivity, the temperature at any depth z and time t can be estimated by the following expression 2).
In this expression, the unit of time, t, and phase constant of the soil surface, t0, should be converted into days. Similarly, the unit of soil thermal diffusivity, αs, should also be converted into m2/days.
By integrating the expression with respect to depth, the average temperature of a vertical soil profile ranging between depth z1and z2 (°C ) can be determined as follows 2).
where,
As the final step with regard to the heat transfer between soil and earth tube system, thermal conductivity of air (W/m°C), kair, and kinetic viscosity of air (m2/s), υ, should calculated first 3).
By using the values of thermal conductivity of air, kair, and kinetic viscosity of air, υ, the convective heat transfer coefficient at the inner pipe surface (W/m2°C), hc, can be evaluated. It is a function of Reynolds number, Re, and Nusselt number, Nu 4), where
where r1 is inner pipe radius (m), and Va is average pipe air velocity (m/s).
After determining the convective heat transfer coefficient, Rc, Rp and Rs are respectively calculated as follows.
where Rc is thermal resistance due to convection heat transfer between the air in the pipe and the pipe inner surface (m-C/W), Rp is thermal resistance due to conduction heat transfer between the pipe inner and outer surface (m-C/W), and Rs is thermal resistance due to conduction heat transfer between the pipe outer surface and undisturbed soil (m-C/W). In addition r2 is pipe thickness (m), r3 is distance between the pipe outer surface and undisturbed soil (m), and L is pipe length (m).
Finally, the heat transfer between the soil and the air inside the pipe is equal to the amount of heat losses as air flows along the pipe (Jacovides and Mihalakakou, 1995).
with
where Ut is overall heat transfer coefficient of the whole earth tube system (W/C-m), Ta(y) is air temperature of the pipe at the distance y from the pipe inlet (°C), and ma is mass flow rate of ambient air through pipe (kg/s). Ca is specific heat of air (J/kg°C) and Rt is total thermal resistance between pipe air and soil (m-C/W).
Initial condition of inlet air temperature is equal to the ambient air temperature. Outlet air temperature is finally evaluated by solving the heat transfer equation above.
Table: Nomenclature for Earthtube Model
Variable|Description|Units ——–|———–|—– As amplitude of the soil surface temperature variation (°C)
Ca specific heat of air (J/kg°C)
hc convective heat transfer coefficient at the inner pipe surface (W/m2°C)
hs convective heat transfer coefficient at the soil surface (W/m2°C)
kair thermal conductivity of the air (W/m°C)
kp pipe thermal conductivity (W/m°C)
ks soil thermal conductivity (W/m°C)
L pipe length (m)
ma mass flow rate of ambient air through pipe (kg/s)
ra relative humidity
Rc thermal resistance due to convection heat transfer between the air in the pipe and the pipe inner surface (m-C/W)
Rp thermal resistance due to conduction heat transfer between the pipe inner and outer surface (m-C/W)
Rs thermal resistance due to conduction heat transfer between the pipe outer surface and undisturbed soil (m-C/W)
Rt total thermal resistance between pipe air and soil (m-C/W)
ΔR radiation constant (63W/m2)
r1 inner pipe radius (m)
r2 pipe thickness (m)
r3 distance between the pipe outer surface and undisturbed soil (m)
Sm average solar radiation (W/m2)
Sv amplitude of the solar radiation (W/m2)
t time elapsed from beginning of calendar year (days)
Ta(y) air temperature of the pipe at the distance y from the pipe inlet (°C)
Tm average soil surface temperature (°C)
Tma average air temperature (°C)
t0 phase constant of the soil surface (sec; days)
t0a phase constant of the air (sec; days)
Tva amplitude of the air temperature (°C)
Tz,t~~ ground temperature at time t and depth z (°C)
Tz1,z2,t~~ soil profile temperature at time t, averaged over depths between z1 and z2 (°C)
u wind velocity above the ground surface (m/s)
Ut overall heat transfer coefficient of the whole earth tube system (W/m-C)
Va average pipe air velocity (m/s)
z depth of the radial center of pipe below soil surface (m)
z1 upper bounds of some vertical profile in soil (m)
z2 lower bounds of some vertical profile in soil (m)
αs soil thermal diffusivity (m2/s; m2/days)
β soil absorption coefficient (= 1 – soil albedo)
ε hemispherical emittance of the ground surface
φI phase angle between the insolation and the air temperature (rad)
Φs phase angle difference between the air and soil surface temperature (rad)
υ kinetic viscosity of air (m2/s)
w annual angular frequency (=1.992 x 10-7rad/s)
Krarti M., Lopez-Alonzo C., Claridge D. E. and Kreider J. F. 1995. Analytical model to predict annual soil surface temperature variation. Journal of Solar Energy Engineering 117, 91~99
Labs K. In: Cook J., editor. 1989. Passive cooling. Cambridge Massachusetts, London, England: MIT Press
Al-Ajmi F., Loveday D. L. and Hanby V. I. 2005. The Cooling Potential of Earth-air Heat Exchangers for Domestic Buildings in a Desert Climate, Building and Environment
Necati Ozisik M. 1885. Heat transfer: A basic approach, McGraw-Hill Book Company
Jacovides C. P. and Mihalakakou G. 1995. An Underground Pipe Systems as an Energy Source for Cooling/Heating Purposes. Renewable Energy 6, pp.893~900
Thermal Chimney Model[LINK]
The ZoneThermalChimney input object is available for modeling a thermal chimney which is a device that uses stack driven air movement to ventilate spaces within a building. These systems have been used successfully in buildings as small as the size of an outhouse up to large commercial buildings. The air within a thermal chimney is heated naturally using solar energy. The air increases in temperature which causes its density to drop. This drop in density results in a natural vertical movement of air and a local drop in pressure. The drop in pressure is relieved by drawing air from the building interior, and the heat gained within the thermal chimney does not enter the occupied portion of the building. These systems are often used in support of natural ventilation systems. The EnergyPlus model will seek to model the air heat balance effects of the thermal chimney, balance air movements caused by the thermal chimney, and report other appropriate system variables. The new model will be linked into the air heat balance in a fashion similar to the current infiltration and simple ventilation models but will not be linked to an HVAC air loop. Any flow through the thermal chimney will be accounted for in the air mass balance in the HVAC calculations. However, other sophisticated ventilation strategies can be handled by other existing EnergyPlus components.
Thermal Chimney Input Requirements
- Distance from the top of thermal chimney to each inlet (m),
- Relative ratio of air flow rates passing through each inlet,
- Width of the absorber wall (m),
- Discharge coefficient,
- Cross sectional area of air channel outlet (m2),
Cross sectional areas of each air channel inlet (m2)
Assumptions
- Surface temperature of the glass cover is uniformly distributed.
- Surface temperature of the absorber wall is uniformly distributed.
- The inlet temperature of the air channel in the thermal chimney is equal to the room air temperature.
- Resistance to the air flow due to the surface friction is negligible.
The discharged amount of interior air induced by the thermal chimney is replaced by the outdoor air infiltration.
Mathematical model currently available for thermal chimneys has the capability to handle the thermal chimney having only one inlet. In other words, it is unlikely that thermal chimneys with multiple inlets due to multiple stories utilizing the common thermal chimney can be mathematically modeled without computational fluid dynamics. Therefore, if the thermal chimney to be modeled has multiple inlets, it will be assumed that it will have only one inlet. For this assumption, the user will be required to specify the relative ratio of air flow rates passing through each inlet to compute the overall length of the thermal chimney (m), L, overall room air temperature (K), Tr, and overall cross sectional area of air channel inlet (m2), Ai, as follows:
Where, Ain is the cross sectional area of nth air channel inlet (m2), Ln is the distance from the top of thermal chimney to nth inlet (m), En is the room air specific enthalpy corresponding to nth inlet (J/kg), rn is the relative ratio of air flow rate passing through nth inlet and Trn is the room air temperature corresponding to nth inlet (K). Among them, room air specific enthalpy, En, and room air temperature corresponding to each inlet, Trn, are directly calculated inside EnergyPlus. In addition, the relative ratios should meet the following expression:
After merging the multiple inlets into a single inlet condition based on the description above, the following algorithm which is widely used is employed for the modeling of the thermal chimney.
The key output parameter in the thermal chimney model is the enhanced amount of natural ventilation rate caused by the presence of a thermal chimney. In order to determine the enhanced ventilation, the discharge air temperature from a thermal chimney should be calculated, which, in turn, should be computed based on the information on the absorber wall temperature, glass cover temperature and the vertical air temperature distribution within the thermal chimney. Among them, energy balances for the absorber wall and the glass cover are carried out using the existing algorithm currently available in EnergyPlus, which has the similar approach to the Trombe wall. On the other hand, the vertical air temperature distribution and the resultant discharge air temperature of the thermal chimney are computed using the separate thermal chimney algorithm described in the following paragraphs.
Once the glass cover temperature and the absorber wall temperature are computed using the existing modeling algorithm in EnergyPlus, the energy balance for the fluid (air inside the thermal chimney) can be expressed as:
Where, m is the total mass flow rate of the air (kg/s), Cp is the specific heat of air (J/kg°C), w is the width of the absorber wall (m) and x is the elemental length of the absorber wall (m).
Since the initial condition of inlet air temperature in this differential equation is equal to the room air temperature (i.e. x = 0, Tf,i = Tr), the outlet air temperature, Tfo, can be finally evaluated.
Finally, the total air flow rate caused by the thermal chimney (m3/s), Q, can be evaluated from the following expression [1]:
Where, Cd is the discharge coefficient, Ao and Ai is the cross sectional areas of air channel outlet and inlet (m2), respectively, Tfo is the outlet air temperature (K), Tr is the room air temperature (K) and L is the total length of the thermal chimney (m).
Since multiple inlets are merged into a single inlet in the beginning, the air flow rate passing through each inlet due to the existence of the thermal chimney can be finally determined as follows:
 ,
,  ,
, 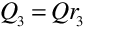 , ∙∙∙,
, ∙∙∙, 
Where, Qn is the air flow rate passing through nth inlet (m3/s) and rn is the relative ratio of air flow rate passing through nth inlet.
The discharged amount of interior air from each zone caused by the presence of the thermal chimney is assumed to be replaced by the outdoor air infiltration.
Nomenclature of Thermal Chimney Model
| Variable |
| ——– |
| Ai |
| Ao |
| Cd |
| Cp |
| En |
| g |
| hgam |
| hgf |
| hiw |
| hwf |
| hwind |
| Hsr |
| kair |
| L |
| M |
| rn |
| Sg |
| Sw |
| Tam |
| Tf |
| Tfi |
| Tfo |
| Tg |
| Tr |
| Ts |
| Tw |
| T∞ |
| u |
| Uw |
| w |
| x |
| αg |
| αw |
| β |
| εg |
| σ |
| τ |
| v |
N. K. Bansal, R. Mathur and M. S. Bhandari, Solar Chimney for enhanced Stack Ventilation, Building and Environment, 28, pp.373-377, 1993
K. S. Ong, A Mathematical Model of a Solar Chimney, Renewable Energy, 28, pp.1047-1060, 2003
N. K. Bansal, R. Mathur and M. S. Bhandari, A Study of Solar Chimney Assisted Wind Tower System for Natural Ventilation in Buildings, Building and Environment, 29, pp.495-500, 1994
J. Marti-Herrero and M. R. Heras-Celemin, Dynamic Physical Model for a Solar Chimney, Solar Energy, 81, pp. 614-622, 2007
M. M. Aboulnaga and S. N. Abdrabboh, Improving Night Ventilation into Low-rise Buildings in Hot-arid Climates Exploring a Combined Wall-roof Solar Chimney, Renewable Energy, 19, pp. 47-54, 2000
Zone Outdoor Air Unit[LINK]
The zone outdoor air unit (object ZoneHVAC:OutdoorAirUnit) is intended to model systems such as zone make-up air units and dedicated outside air systems. These components are “zone equipment” meaning that they do not require an air loop but serve a zone directly. The system is comprised of a supply fan (in either draw through or blow through configuration), an optional exhaust fan, and a variety of components such as heating coils, cooling coils, heat recovery, etc. The object of the zone outdoor air unit is to bring in additional ventilation air into a zone. These might be used for high ventilation spaces such as kitchens or laboratories where another system is primarily responsible for space conditioning while the zone outside air unit is primarily responsible for fresh air delivery to the zone. Most of the information necessary to configure a zone outdoor air unit is contained in the EnergyPlus Input/Output Reference. A diagram of the zone outdoor air unit is shown below. As this system is relatively simple and does not contain any unique operating algorithm or equations, the discussion here is limited to the application of the user defined controls and how it relates to the operation of the device.
Three input parameters control the operation of the zone outdoor air unit. The unit control type has two options: neutral or temperature. If the temperature control type is selected, the user must also provide a high and low air temperature control schedule. The algorithm for controlling the zone outdoor air unit is dependent on these parameters which are used as described below.
Neutral Control. If the user selects neutral control, the intent is to provide additional outside air to the zone without imposing any additional thermal load on the zone or any other systems serving the zone. In other words, the unit will attempt to provide air to the zone at the zone mean air temperature. Mathematically, this means:
where:
Tout = the outlet temperature of the zone outdoor air unit
TMAT = the mean air temperature of the zone being served by the unit
It should be noted that to avoid excessive iteration that the zone mean air temperature that is used is the mean air temperature from the previous time step. This will result in a slight lagging that may introduce a slight thermal load, but this should be minimal.
Temperature Control. If the user selects temperature control, the intent is to limit the outlet temperature of the unit for either heating or cooling or both or perhaps to provide unconditioned air to the space. The algorithm used to determine the outlet temperature of the unit is as follows. When the outdoor air temperature is at or below the low air temperature control schedule value, the outlet temperature is set to the low air temperature control schedule value and any heating equipment included in the unit description and available will attempt to provide enough heating to produce an outlet temperature equal to the low temperature schedule value. When the outdoor air temperature is at or above the high air temperature control schedule value, the outlet temperature of the unit is set to the high air temperature control schedule value and any cooling equipment included in the unit description and available will attempt to provide enough cooling to produce an outlet air temperature equal to the high temperature schedule value. When the outdoor air temperature is between the high and low temperature values, the unit will not provide any conditioning of outdoor air and will simply deliver it to the zone. Mathematically, this can be summarized as:
where:
Tout = the outlet temperature of the zone outdoor air unit
Toa = the outside air temperature
Thigh = the high control air temperature schedule value
Tlow = the low control air temperature schedule value
If the user wishes to provide “unconditioned” air all of the time, the high and low control temperature values can be set very high and very low, respectively, to always force the unit to provide unconditioned air. The same effect can also be realized by not specifying any conditioning components (such as coils) in the unit. The user can also limit the device to cooling only by specifying a low control temperature schedule with extremely low values. Conversely, the user can limit the device to heating only by specifying a high control temperature schedule with extremely high values. The user can also limit the equipment specified as part of the device to either cooling or heating components to get similar effects. In essence, the temperature control provides a variety of options in a single control type through the use of the high and low control temperature schedules.
Zone Exhaust Fan[LINK]
The zone exhaust fan (Fan:ZoneExhaust) is a simple model to account for the fan electric energy use and impact on central air handlers from bathroom and hood exhaust. Because the fan only extracts air from the zone, it doesn’t directly impact the zone itself.
The fan flow rate is either constant or variable depending on if the user input a flow fraction modifier schedule. The value entered for maximum volume flow rate is converted to a design mass flow rate using standard (altitude-adjusted) density and used as the design flow rate. If a flow fraction schedule is used, then its values, fFract, are multiplied by the design flow rate to obtain the current mass flow.
The exhaust fan model is similar to, but simpler than, the models used for air system fans. The electric power calculation is simplified and uses a constant overall efficiency. All of the fan power is added to the air stream.
The controls for determining if the the exhaust fan will operate can be based on a number of factors including: an on/off availability schedule, interaction with system availability managers, minimum zone air temperature control limits and a variable flow fraction schedule. When the fan is coupled to the system availability managers then it will operate if either the local availability schedule or the system availability manager’s indicate that the fan should run. When the fan is not coupled to the system availability manager, then it only uses the local availability schedule and ignores availability managers. If using the flow fraction schedule and the resulting flow is zero, then fan will not run. If using the minimum zone temperature limit schedule then the fan will only run if the fan inlet temperature is warmer than the limit.
The exhaust fan’s interaction with the air system depends on the value, fBal, of the schedule for the fraction of the exhaust that is balanced. The model tracks the exhaust flows in two ways, balanced and unbalanced. Balanced exhaust air flow is considered to have been made up from simple airflow from infiltration, ventilation or zone mixing. Unbalanced exhaust air flow is considered to not be balanced by simple air flows and needs to be balanced by the air system operation. Both of these types of flow are summed at the zone and whole air system level. In a zone, the return air node flow rate is reduced from what it would be with no exhaust by the portion of the zone’s exhaust flow that is unbalanced. In an air handler with an outdoor air system, the outdoor air flow rate may be increased so as to be sufficient to provide all the unbalanced exhaust air for all the zones on the air handler (when possible).
Zone Equipment and Zone Forced Air Units[LINK]
Air Distribution Terminal Unit[LINK]
Overview[LINK]
The ZoneHVAC:AirDistributionUnit is a special piece of zone equipment – it connects centrally conditioned air with a zone. It encompasses the various types of air terminal units in EnergyPlus: AirTerminal:DualDuct:ConstantVolume, AirTerminal:SingleDuct:VAV:Reheat, etc. It is a generalized component that accesses the calculations for the different types of air terminal unit.
Model[LINK]
The air distribution function is encapsulated in the module ZoneAirEquipmentManager. The object and module function only to invoke the individual air terminal unit simulations.
Inputs and Data[LINK]
The data for this unit consists of the unit name, the air outlet node name (which should be the same as one of the zone inlet nodes), the type of air terminal unit (air distribution equipment), and the name of the air terminal unit.
All input data for air distribution units is stored in the array AirDistUnit in data module DataDefineEquip.
Calculation[LINK]
There is no calculation associated with ZoneHVAC:AirDistributionUnit.
Simulation and Control[LINK]
SimZoneAirLoopEquipment in module ZoneAirEquipmentManager calls the individual air terminal unit simulations.
References[LINK]
No specific references.
Simple Duct Leakage Model[LINK]
Overview[LINK]
The input object ZoneHVAC:AirDistributionUnit also provides access to a model for duct leakage that can be a significant source of energy inefficiency in forced-air HVAC systems. Evaluating duct leakage energy losses can involve considerable user effort and computer resources if an airflow network is defined through a detailed description of the system components and airflow paths (including leakage paths). A nonlinear pressure-based solver is used to solve for pressures and flow rates in the network. By making certain assumptions and approximations for certain well defined configurations, however, it is possible to obtain accurate results with a simple mass and energy balance calculation and thus avoid the input and calculation costs of doing a full pressure-based airflow network simulation.
The Simple Duct Leakage Model (SDLM) assumes a central VAV air conditioning system with a constant static pressure setpoint. The model assumes that the leaks are in the supply ducts and that the system returns air through a ceiling plenum that contains the ducts. Thus, the ducts leak into the return plenum, and this part of the supply does not reach the conditioned zones. With the additional assumptions described below, it is possible to model this configuration with heat and mass balance equations and avoid the use of a nonlinear pressure-based solver. In the EnergyPlus context, this means that use of AirflowNetwork is avoided and the leakage calculations are obtained in the course of the normal thermal simulation.
Principles and Description[LINK]
Constant Flow Rate
The airflow rate through a duct leak is a function of the pressure difference between the duct and the surrounding space:
The exponent n is 0.5 for leaks that look like orifices (holes that are large relative to the thickness of the duct wall); for leaks that resemble cracks (e.g., lap joints), n is approximately 0.6 to 0.65.
For a duct with constant flow rate and a linear pressure drop through the duct, the average static pressure in the duct will equal half of the duct static pressure drop. Assuming turbulent flow in the duct, the duct pressure drop is proportional to the square of the airflow through the duct. This can be expressed as:
Combining equations and and assuming the leaks are large holes (n equals 0.5). gives:
where
Thus the leakage fraction C3 remains constant regardless of the duct flow rate or static pressure. This result depends on the following assumptions:
the duct airflow is turbulent;
the duct pressure varies linearly along the duct;
the average duct pressure approximates the pressure drop across the duct;
the leaks are large and have pressure exponent 0.5.
Effects of Constant Pressure Upstream and Variable Flow and Pressure Downstrean
Commonly VAV systems maintain a constant static pressure at some point in the duct system upstream of the VAV terminal units. That is, airflow rate will vary depending on the cooling requirement, but a constant pressure will be maintained at the static pressure sensor. Consequently, the leakage flow for a leak upstream of the VAV boxes will be approximately constant. Or to put it another way, the leakage fraction will vary in proportion to the flow rate.
For leaks downstream of the VAV terminal units, the airflow through the duct and the pressure in the downstream duct will vary as the box damper modulates in response to the differential between the room temperature and the thermostat setpoint. In this case, the situation is similar to the constant flow case: for an orifice-like leak, the pressure difference across the leak will vary linearly with the air speed (or flow rate); i.e., the leakage fraction will be approximately constant.
SDLM
For SDLM, our leakage model is then:
for leaks upstream of the terminal units, the leakage flow rate will be constant;
for leaks downstream of the terminal units, the leakage fraction will be constant.
This model assumes, in addition to the assumptions given above, that the VAV system is controlled to a constant static pressure setpoint. In EnergyPlus SDLM is not currently applicable to systems using static pressure reset. Using SDLM would require knowledge of static pressure as a function of system air flow rate.
Inputs and Data[LINK]
User data for the SDLM is entered through The ZoneHVAC:AirDistributionUnit (ADU) object. There are 2 data items per ADU:
the upstream nominal leakage fraction;
the downstream fixed leakage fraction.
Both inputs are leakage fractions. Input (1) is the leakage fraction at design flow rate, which together can be used to determine the constant leakage flow rate upstream of the VAV boxes; this leakage fraction varies with the flow rate. Input (2) is a fixed leakage fraction and is constant as the flow rate varies.
Implementation[LINK]
The various zone mass flow rates are related in the following manner.
Here
Downstream leakage must also be accounted for because not all of will reach the zone. This is done by having
will reach the zone. This is done by having  meet an adjusted zone load:
meet an adjusted zone load:
Here [watts] is the actual zone load (met by
[watts] is the actual zone load (met by  ) and
) and  is the load used in the VAV terminal unit model to obtain
is the load used in the VAV terminal unit model to obtain  .
.
Once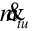 is known, all the other flow rates can be calculated.
is known, all the other flow rates can be calculated.  is assigned to the air distribution unit’s air inlet node and
is assigned to the air distribution unit’s air inlet node and  is assigned to the unit’s air outlet node. Thus, air mass flow is not conserved through the unit: the two air leakage flow rates disappear. These two vanished flow rates are stored in the air distribution unit data structure. When the downstream return air plenum mass and energy balances are calculated, the leakage flow rate data is accessed and added back in as inlets to the return air plenum. Thus, the overall air system preserves a mass balance.
is assigned to the unit’s air outlet node. Thus, air mass flow is not conserved through the unit: the two air leakage flow rates disappear. These two vanished flow rates are stored in the air distribution unit data structure. When the downstream return air plenum mass and energy balances are calculated, the leakage flow rate data is accessed and added back in as inlets to the return air plenum. Thus, the overall air system preserves a mass balance.
References[LINK]
Wray, C.P. 2003. “Duct Thermal Performance Models for Large Commercial Buildings”, Lawrence Berkeley National Laboratory Report to the California Energy Commission. LBNL-53410.
Wray, C.P. and N.E. Matson. 2003. “Duct Leakage Impacts on VAV System Performance in California Large Commercial Buildings”, Lawrence Berkeley National Laboratory Report to the California Energy Commission. LBNL-53605.
Wray, C.P., R.C. Diamond, and M.H. Sherman. 2005. “Rationale for Measuring Duct Leakage Flows in Large Commercial Buildings”. Proceedings – 26th AIVC Conference, Brussels, Belgium, September. LBNL-58252.
Fan Coil Unit[LINK]
Window Air Conditioner[LINK]
Packaged Terminal Air Conditioner[LINK]
Packaged Terminal Heat Pump[LINK]
Zone Single Speed Water-To-Air Heat Pump[LINK]
Overview[LINK]
The input object ZoneHVAC:WaterToAirHeatPump provides a zone equipment model for a water-to-air heat pump that is a “virtual” component consisting of an on/off fan component, a water-to-air heat pump cooling coil, a water-to-air heat pump heating coil, and a gas or electric supplemental heating coil. The specific configuration of the blowthru heat pump is shown in the following figure. For a drawthru heat pump, the fan is located between the water-to-air heat pump heating coil and the supplemental heating coil. In addition, a water-to-air heat pump has a water loop connection on its source side. The water loop can be served by a condenser loop (like GHE for Ground source systems), or by a cooling tower/ boiler plant loop (for water loop systems).
There are two models for zone water-to-air heat pump cooling and heating coils, i.e. Single-Speed and Variable-Speed Equation Fit models. Cooling and heating coils are modeled using the Equation Fit model described here.
Single Speed Equation-Fit Model:[LINK]
This section describes the equation-fit model for Water-to-Air heat pump (Object names: Coil:Cooling:WaterToAirHeatPump:EquationFit andCoil:Heating:WaterToAirHeatPump:EquationFit). This documentation is derived from the M.S. dissertation of Tang (2005) which is available on the Oklahoma State University web site http://www.hvac.okstate.edu/. The model uses five non-dimensional equations or curves to predict the heat pump performance in cooling and heating mode. The methodology involves using the generalized least square method to generate a set of performance coefficients from the catalog data at indicated reference conditions. Then the respective coefficients and indicated reference conditions are used in the model to simulate the heat pump performance. The variables or inlet conditions that influenced the water-to-air heat pump performance are load side inlet water temperature, source side inlet temperature, source side water flow rate and load side water flow rate. The governing equations for the cooling and heating mode are as following:
Cooling Mode:
Heating Mode:
Assuming no losses, the source side heat transfer rate for cooling and heating mode is calculated as following;
where:
The inlet conditions or variables are divided by the reference conditions. This formulation allows the coefficients to fall into smaller range of values. Moreover, the value of the coefficient indirectly represents the sensitivity of the output to that particular inlet variable. The reference conditions used when generating the performance coefficients must be the same as the reference conditions used later in the model. The reference temperature is fixed at 283K. Temperature unit of Kelvin is used instead of Celsius to keep the ratio of the water inlet temperature and reference temperature positive should the water inlet temperature drop below the freezing point.
is fixed at 283K. Temperature unit of Kelvin is used instead of Celsius to keep the ratio of the water inlet temperature and reference temperature positive should the water inlet temperature drop below the freezing point.
For cooling mode, the reference conditions; reference load side air volumetric flow rate ,reference source side water volumetric flow rate
,reference source side water volumetric flow rate ,reference sensible capacity
,reference sensible capacity  and reference power input
and reference power input 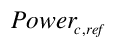 are the conditions when the heat pump is operating at the highest cooling capacity or reference cooling capacity
are the conditions when the heat pump is operating at the highest cooling capacity or reference cooling capacity indicated in the manufacturer’s catalog. Note that the reference conditions for heating mode might differ from the reference conditions specified for the cooling mode.
indicated in the manufacturer’s catalog. Note that the reference conditions for heating mode might differ from the reference conditions specified for the cooling mode.
Coefficient estimation procedure:[LINK]
The generalized least square method is used to generate the coefficients. This method utilizes an optimization method which calculates the coefficients that will give the least amount of differences between the model outputs and the catalog data. A set of coefficients for the cooling mode is generated which includes A1-A5 for total cooling capacity, B1-B6 for sensible cooling capacity, and C1-C5 for power consumption. The same procedure is repeated for the heating mode to generate the coefficients E1-E5 (total heating capacity) and F1-F5 (power consumption). An information flow chart showing the inputs, reference conditions, performance coefficients and outputs are shown in the figure below:
Zone Air DX Dehumidifier[LINK]
Overview[LINK]
This model, object name ZoneHVAC:Dehumidifier:DX, simulates the thermal performance and electric power consumption of conventional mechanical dehumidifiers. These systems use a direct expansion (DX) cooling coil to cool and dehumidify an airstream. Heat from the DX system’s condenser section is rejected into the cooled/dehumidified airstream, resulting in warm dry air being supplied from the unit. In EnergyPlus, this object is modeled as a type of zone equipment (ref. ZoneHVAC:EquipmentList and ZoneHVAC:EquipmentConnections).
The model assumes that this equipment dehumidifies and heats the air. If used in tandem with another system that cools and dehumidifies the zone air, then the zone dehumidifier should be specified as the lowest cooling priority in the ZoneHVAC:EquipmentList object for best control of zone temperature and humidity levels. With this zone equipment prioritization, the other cooling and dehumidification system would operate first to meet the temperature setpoint (and possibly meet the high humidity setpoint as well). If additional dehumidification is needed, then the zone dehumidifier would operate. The sensible heat generated by the dehumidifier is carried over to the zone air heat balance for the next HVAC time step.
Model Description[LINK]
The user must input water removal, energy factor and air flow rate at rated conditions (26.7°C, 60% RH). Three performance curves must also be specified to characterize the change in water removal and energy consumption at part-load conditions:
where
Tin = dry-bulb temperature of the air entering the dehumidifier, °C
RHin = relative of the air entering the dehumidifier, % (0-100)
or
where
The part load fraction correlation should be normalized to a value of 1.0 when the part load ratio equals 1.0 (i.e., no efficiency losses when the dehumidifier runs continuously for the simulation timestep). For PLR values between 0 and 1 (0 <= PLR < 1), the following rules apply:
0.7 <= PLF <= 1.0 and PLF >= PLR
If PLF < 0.7 a warning message is issued, the program resets the PLF value to 0.7, and the simulation proceeds. The runtime fraction of the dehumidifier is defined as PLR/PLF. If PLF < PLR, then a warning message is issued and the runtime fraction of the dehumidifier is set to 1.0.
Mechanical dehumidifier typically have long runtimes with minimal compressor cycling. So, a typical part load fraction correlation might be:
PLF = 0.95 + 0.05(PLR)
If the user wishes to model no efficiency degradation due to compressor cycling, the part load fraction correlation should be defined as follows:
PLF = 1.0 + 0.0(PLR)
All three part-load curves are accessed through EnergyPlus’ built-in performance curve equation manager (Curve:Quadratic, Curve:Cubic and Curve:Biquadratic). It is not imperative that the user utilize all coefficients shown in curve equations above if their performance equation has fewer terms (e.g., if the user’s PartLoadFrac performance curve is linear instead of quadratic, simply enter the values for a and b, and set coefficient c equal to zero).
For any simulation time step when there is a water removal load to be met, the dehumidifier is available to operate (via availability schedule), and the inlet air dry-bulb temperature is within the minimum and maximum dry-bulb temperature limits specified in the input file for this object, the water removal rate for the dehumidifier is calculated as follows:
where
The Zone Dehumidifier Part-Load Ratio (output variable) is then calculated, with the result constrained to be from 0.0 to 1.0:
The steady-state and average electrical power consumed by the dehumidifier are calculated next using the following equations:
where
If the dehumidifier is unavailable to operate for the time period (via the specified availability schedule) then Zone Dehumidifier Electric Power is set equal to zero.
The average water removal rate (kg/s) for the simulation time step is then calculated:
The Zone Dehumidifier Sensible Heating Rate (output variable) is calculated as follows:
where
hfg = enthalpy of vaporization of air, J/kg
The air mass flow rate through the dehumidifier is determined using the Rated Air Flow Rate (m3/s) entered in the input, PLR, and converting to mass using the density of air at rated conditions (26.7C, 60% RH) and local barometric pressure accounting for altitude
p=101325*(1-2.25577E-05*Z)**5.2559 where p=pressure in Pa and Z=altitude in m:
where
The dry-bulb temperature and humidity ratio of the air leaving the dehumidifier are calculated as follows:
where
Tout =Zone Dehumidifier Outlet Air Temperature, C (output variable). Represents the
outlet air temperature when the dehumidifier is operating.
Tin = inlet air dry-bulb temperature, C
win = inlet air humidity ratio, kg/kg
wout = outlet air humidity ratio, kg/kg
If the dehumidifier does not operate for a given HVAC simulation time step, then the outlet air dry-bulb temperature and humidity ratio are set equal to the corresponding inlet air values.
Finally, the following additional output variables are calculated:
where
Qsensible~~= output variable ‘Zone Dehumidifier Sensible Heating Energy [J]’
Edehumid = output variable ‘Zone Dehumidifier Electric Energy [J]’
Poff-cycle,avg = output variable ‘Zone Dehumidifier Off Cycle Parasitic Electric Power [W]’
Eoff-cycle = output variable ‘Zone Dehumidifier Off Cycle Parasitic Electric Energy [J]’
mwater~~= output variable ‘Zone Dehumidifier Removed Water Mass [kg]’
Energy Recovery Ventilator[LINK]
The input object ZoneHVAC:EnergyRecoveryVentilator provides a model for a stand alone energy recovery ventilator (ERV) that is a single-zone HVAC component used for exhaust air heat recovery (see figure below). This compound object consists of three required components: a generic air-to-air heat exchanger (see object HeatExchanger:AirToAir:SensibleAndLatent), a supply air fan, and an exhaust air fan (see object Fan:OnOff). An optional controller (see object ZoneHVAC:EnergyRecoveryVentilator:Controller) may be used to simulate economizer (free cooling) operation.
This compound object models the basic operation of supply and exhaust air fans and an air-to-air heat exchanger. The stand alone ERV operates whenever the unit is scheduled to be available (Availability schedule). The stand alone ERV object can be used in conjunction with an economizer feature whereby heat exchange is suspended whenever free cooling is available (i.e., air flow is fully bypassed around a fixed-plate heat exchanger or the rotation of a rotary heat exchanger is stopped).
To model a stand alone ERV connected to a single zone, the input data file should include the following objects:
Model Description[LINK]
The purpose of this compound component is to simply call the individual component models and optional controller for each energy recovery ventilator. Since this equipment is not associated with an air loop, the compound object sets the supply and exhaust air mass flow rates through the ventilator. This compound object is also used to report the total, sensible and latent energy supplied to the zone, as well as the total electrical energy consumed by all of the individual components (supply air fan, exhaust air fan and heat exchanger parasitics).
During each similation time step, the air mass flow rate at the supply air and exhaust air inlets is set based on the stand alone ERV’s availablility schedule and the specified volumetric air flow rates as follows:
IF (availability schedule value > 0) THEN
ELSE
where:
With the supply and exhaust inlet air mass flow rates set, the compound object then calls the generic air-to-air heat exchanger model to determine its supply air and exhaust air exiting conditions based on the inputs specified in the heat exchanger object. The supply air and exhaust air fans are then modeled to determine the final conditions of the air streams exiting the stand alone energy recovery ventilator. The heat exchanger and fan models are described in detail elsewhere in this document (reference: HeatExchanger:AirToAir:SensibleAndLatent and Fan:OnOff).
The sensible heat transfer rate to the zone by the stand alone ventilator is then calculated as follows:
where:
hSupplyOutlet = enthalpy of the air being supplied to the zone, J/kg
hExhaustInlet~~= enthalpy of the air being exhausted from the zone through the ventilator, J/kg
HRmin = enthalpies evaluated at a constant humidity ratio, the minimum humidity ratio
of the supply air outlet or the exhaust air inlet
The resulting sensible energy transfer rate is passed to the zone equipment manager and added to the zone load to be met by other heating or cooling equipment. Since the stand alone ERV is intended to reduce the outdoor air load through heat exchange and not meet that load completely, the stand alone heat exchanger must be modeled first in the list of zone equipment. This is accomplished by setting the stand alone ERV priority for cooling and heating higher than that of other zone cooling or heating equipment (reference: ZoneHVAC:EquipmentList).
When economizer (free cooling) operation is desired, a controller is coupled to the stand alone ERV by providing the name of the controller object in the ERV controller input field. This controller determines when the air-side economizer is active (i.e., air flow is fully bypassed around a fixed-plate heat exchanger or the rotation of a rotary heat exchanger is stopped) based on the controller inputs (Ref. ZoneHVAC:EnergyRecoveryVentilator:Controller).
At the end of each HVAC simulation time step, this compound object reports the heating or cooling rate and energy delivered to the zone, as well as the electric power and consumption by the ventilator. In terms of thermal energy delivered to the zone, the sensible, latent and total energy transfer rate to the zone is calculated as follows:
where:
hSupplyOutlet = enthalpy of the air being supplied to the zone, J/kg
hExhaustInlet~~= enthalpy of the air being exhausted from the zone through the ventilator, J/kg
HRmin = enthalpies evaluated at a constant humidity ratio, the minimum humidity ratio
of the supply air outlet or the exhaust air inlet
Since each of these energy transfer rates can be calculated as positive or negative values, individual reporting variables are established for cooling and heating and only positive values are reported. The following calculations are representative of what is done for each of the energy transfer rates:
IF ( < 0.0 ) THEN
< 0.0 ) THEN
ELSE
where:
In addition to heating and cooling rates, the heating and cooling energy supplied to the zone is also calculated for the time step being reported. The following example for total cooling energy is representative of what is done for the sensible and latent energy as well as the heating counterparts.
where:
TimeStepSys = HVAC system simulation time step, hr
Unit Heater[LINK]
(Note: Some of this information also appears in the Input Output Reference for EnergyPlus. It is repeated here for clarity.)
The input object ZoneHVAC:UnitHeater provides a model for unit heaters that are zone equipment units which are assembled from other components and are a simplification of unit ventilators. They contain only a fan and a heating coil. These components are described elsewhere in this document. The unit heater input simply requires the names of these components, which have to be described elsewhere in the input. The input also requires the name of an availability schedule, maximum airflow rate, and maximum and minimum hot water volumetric flow rates. The unit is connected to the zone inlet and exhaust nodes by specifying unit inlet and outlet node names. Note that the unit air inlet node should be the same as a zone exhaust node and the unit outlet node should be the same as a zone inlet node.
Controls[LINK]
While the control of the heating coil is similar to the fan coil units and the unit ventilator, the overall control of the unit heater is much different. There are four different modes in which a unit heat can operate based on the user input:
OFF: In this mode, the unit has been scheduled off. All flow rates are set to zero, and the temperatures are set to zone conditions.
NO LOAD OR COOLING/ON-OFF FAN CONTROL: In this mode, the unit is available, but there is no heating load. With On-Off fan control, the fan will only run when there is a heating load. Since there is no heating load in this mode, all flow rates are set to zero, and the temperatures are set to zone conditions. Since the unit heater is designed only to provide heating, the presence of a cooling load signifies that the unit should not be running.
NO LOAD OR COOLING/CONTINUOUS FAN CONTROL: In this mode, the unit is available and the fan is controlled to be running continuously. If it is scheduled to be available, the fan runs and circulates air to the space. While no direct heating is provided, any heat added by the fan is introduced into the space with the circulation of the air. If the fan is scheduled off, the fan will not run (this is identical to on-off control with no load).
HEATING: In this mode, the unit and fan are on/available, and there is a heating load. The heating coil is modulated (constant fan speed) to meet the heating load. Control of the heating coil and its flow rate is identical to the fan coil unit and unit ventilator. The flow rate of air through the unit is controlled by the user input and schedules.
Unit Ventilator[LINK]
(Note: Some of this information also appears in the Input Output Reference for EnergyPlus. It is repeated here for clarity.)
The input object ZoneHVAC:UnitVentilator provides a model for unit ventilators that are zone equipment units which are assembled from other components. They contain a built-in outdoor air mixer, a fan, a heating coil, and a cooling coil. These components are described elsewhere in this document, except the built-in outdoor air mixer which is contained within the unit ventilator statement. The unit ventilator input simply requires the names of these other three components, which have to be described elsewhere in the input. The input also requires the name of an availability schedule, maximum airflow rate, outdoor air control information (control type and schedules), an outdoor airflow rate, and maximum and minimum hot and cold water mass flow rates. The unit is connected to the zone inlet and exhaust nodes and the outdoor air by specifying unit inlet, outlet, outdoor air and exhaust (relief) air node names. Note that the unit air inlet node should be the same as a zone exhaust node and the unit outlet node should be the same as a zone inlet node. In general, the unit ventilator input is very similar to the fan coil unit input, and the unit is connected to a hot water loop (demand side) through its hot water coil and to a chilled water loop (demand side) through its cooling coil.
Controls and Outdoor Air[LINK]
The main difference between the fan coil and unit ventilator input is that the unit ventilator has a built-in outdoor air mixer with its own specialized controls. The outdoor air control type can be selected from one of the following options: “variable percent”, “fixed temperature” or “fixed amount”. In fixed temperature control, the amount of outdoor air is varied between the minimum outdoor air fraction (specified by a schedule) and 100% outdoor air to obtain a mixed air temperature as close as possible to the temperature schedule defined in the input. Variable percent control will also vary the amount of outdoor air between the minimum and maximum fractions (both specified in input by the user) to meet the load without the use of a coil if possible. In fixed amount control, the outdoor air flow rate is fixed to the specified value by the user. In this control strategy, the maximum outdoor air flow rate and schedule are automatically set to be equal to the minimum outdoor air flow rate and schedule. These control types are based on the 2004 ASHRAE Systems and Equipment Handbook (pp. 31.1-31.3) description of unit ventilator systems.
The unit is controlled to meet the zone (remaining) heating or cooling demand. If there is a heating demand, the cooling coil is off and the hot water flow through the heating coil is throttled to meet the demand. The hot water control node must be specified (same as the hot water coil inlet node) as well as maximum and minimum possible hot water volumetric flow rates. If there is a cooling demand from the zone, the hot water coil is off and the chilled water flow through the cooling coil is throttled to meet the load. The cooling coil control node must be specified (same as the cooling coil inlet node) and the maximum and minimum chilled water volumetric flow rates must be given. Finally both heating and cooling require a convergence tolerance, which is the tolerance denoting how closely the fan coil unit will meet the heating or cooling load. The tolerance is always relative to the zone load.
Overall, control of the unit must consider the outdoor air. Here is a more detailed description of the overall unit control:
OFF: Unit is schedule off or there is no load on it. All flow rates are set to zero and the temperatures are set to zone conditions (except for the outdoor air inlet). Outdoor air requirements will not override this condition.
HEATING/NO COIL/VARIABLE PERCENT: The unit is on, there is a heating load, no heating coil is present or it has been scheduled off, and variable percent outdoor air control type has been specified. In this case, the variable percent outdoor air controls what happens with the outdoor air. If the outside temperature is greater than the return temperature, then the outdoor air is set to the maximum as defined by the user input. If the outdoor air temperature is less than the return temperature from the zone, then the outdoor air is set to the minimum outdoor air flow rate as defined by the user. Since a coil is not present to further condition the supply air, the zone simply receives whatever temperature air results from the outdoor air controls.
HEATING/NO COIL/FIXED TEMPERATURE: The unit is on, there is a heating load, no heating coil is present or it has been scheduled off, and fixed temperature has been specified. The unit ventilator tries to use outdoor air as best as possible to meet the temperature goal. If it cannot meet this goal because the temperature goal is not between the zone return temperature and the outdoor air temperature, then the unit ventilator will either use the maximum or minimum outdoor air flow rate.
HEATING/NO COIL/FIXED AMOUNT: The unit is on, there is a heating load, no heating coil is present or it has been scheduled off, and fixed amount control has been specified. The unit ventilator fixes the outdoor air flow rate as defined by the user and sets the maximum and minimum outdoor air flow rate to be equal in order to avoid the variation of outdoor air flow rate between the maximum and minimum values. Since a coil is not present to further condition the supply air, the zone simply receives whatever temperature air results from the outdoor air controls.
HEATING/WITH COIL/VARIABLE PERCENT: The unit is on, there is a heating load, and variable percent control is specified. The outdoor air fraction is set to the minimum outdoor air fraction (schedule based), and the heating coil is activated. The heating coil attempts to meet the remaining load on the zone being served by the unit ventilator.
HEATING/WITH COIL/FIXED AMOUNT: The unit is on, there is a heating load, a heating coil is present and is scheduled on, and fixed amount control has been specified. The unit ventilator fixes the outdoor air flow rate as defined by the user and sets the maximum and minimum outdoor air flow rate to be equal in order to avoid the variation of outdoor air flow rate between the maximum and minimum values. The heating coil then attempts to meet any remaining zone heating load.
COOLING/NO COIL/VARIABLE PERCENT: The unit is on, there is a cooling load, no coil is present or it has been scheduled off, and variable percent outdoor air control type has been specified. In this case, the variable percent outdoor air controls what happens with the outdoor air. If the outside temperature is greater than the return temperature, then the outdoor air is set to the minimum as defined by the user input. If the outdoor air temperature is less than the return temperature from the zone, then the outdoor air is set to the maximum outdoor air flow rate as defined by the user. This may be somewhat simplistic in that it could result in overcooling of the space. However, since a temperature goal was not established, this is the best that can be done by the simulation. Since a coil is not present to further condition the supply air, the zone simply receives whatever temperature air results from the outdoor air controls.
COOLING/NO COIL/FIXED TEMPERATURE: The unit is on, there is a cooling load, no cooling coil is present or it has been scheduled off, and fixed temperature has been specified. The unit ventilator tries to use outdoor air as best as possible to meet the temperature goal. If it cannot meet this goal because the temperature goal is not between the zone return temperature and the outdoor air temperature, then the unit ventilator will either use the maximum or minimum outdoor air flow rate in the same fashion as the variable percent outdoor air control.
COOLING/NO COIL/FIXED AMOUNT: The unit is on, there is a cooling load, no cooling coil is present or it has been scheduled off, and fixed amount control has been specified. The unit ventilator fixes the outdoor air flow rate as defined by the user and sets the maximum and minimum outdoor air flow rate to be equal in order to avoid the variation of outdoor air flow rate between the maximum and minimum values. Since a coil is not present to further condition the supply air, the zone simply receives whatever temperature air results from the outdoor air controls.
COOLING/WITH COIL/VARIABLE PERCENT: The unit is on, there is a cooling load, a coil is present and is scheduled on, and variable percent outdoor air control type has been specified. In this case, the percentage of outdoor air is set to the minimum flow outdoor air flow rate. The coil then attempts to meet any remaining zone load.
COOLING/WITH COIL/FIXED TEMPERATURE: The unit is on, there is a cooling load, a cooling coil is present and is scheduled on, and fixed temperature has been specified. The unit ventilator tries to use outdoor air as best as possible to meet the temperature goal. If it cannot meet this goal because the temperature goal is not between the zone return temperature and the outdoor air temperature, then the unit ventilator will either use the maximum or minimum outdoor air flow rate in the same fashion as the fixed temperature outdoor air control for the “no coil” conditions. The cooling coil then attempts to meet any remaining zone load.
COOLING/WITH COIL/FIXED AMOUNT: The unit is on, there is a cooling load, a cooling coil is present and is scheduled on, and fixed amount control has been specified. The unit ventilator fixes the outdoor air flow rate as defined by the user and sets the maximum and minimum outdoor air flow rate to be equal in order to avoid the variation of outdoor air flow rate between the maximum and minimum values. The cooling coil then attempts to meet any remaining zone cooling load.
Note: the unit ventilator controls are strictly temperature based and do not factor humidity into the equation (not an enthalpy economy cycle but rather a simple return air economy cycle). In addition, temperature predictions are not strict energy balances here in the control routine though in the mixing routine an energy balance is preserved.
Variable Refrigerant Flow Terminal Unit[LINK]
Variable refrigerant flow zone terminal units are used exclusively with variable refrigerant flow (VRF) air conditioning systems (ref: AirConditioner:VariableRefrigerantFlow and ZoneTerminalUnitList). The terminal units operate to satisfy a heating or cooling load in a zone based on a zone thermostat temperature set point. A direct-expansion (DX) cooling and/or DX heating coil is specified depending on the operating mode required. Outdoor ventilation air is modeled with the use of an outside air mixer object. Outside air may be provided to the zone only when the coil is operating or can be supplied continuously even when the coil is not operating. A supply air fan is also required and can be modeled as either draw through as shown in the figure below or as blow through where the fan inlet node would be connected to the outside air mixer mixed air node. If an outside air mixer is not used, the fan inlet node would be connected to the zone exhaust node.
Overview[LINK]
As described previously, the terminal units operate to satisfy a heating or cooling load in a zone based on a zone thermostat temperature set point (Zone Control:Thermostatic). Each simulation time step, EnergyPlus performs a zone air heat balance to determine if cooling or heating is required to meet the zone thermostat set points, excluding any impacts from zone terminal unit operation.
Terminal unit performance is then modeled with all heating/cooling coils off but the supply air fan operates as specified by the user. If the zone air heat balance plus the impact of terminal unit operation with coils off results in no requirement for heating or cooling by the terminal unit coils, or if the terminal unit is scheduled off (via its availability schedule), then the terminal unit coils do not operate and the terminal unit’s part-load ratio output variable is set to 0. If the model determines that cooling or heating is required and the terminal unit is scheduled to operate, the model calculates the part-load ratio of the cooling and heating coils in order to meet the thermostat set point temperature.
The following sections describe the performance calculations for cooling-mode and heating-mode.
Model Description[LINK]
Zone terminal units meet a zone load as determined by a zone thermostat. The DX coils within a zone terminal unit will operate to meet a sensible zone load and all terminal units are controlled to either meet a zone sensible cooling load or a zone sensible heating load. This model does not provide for simultaneous cooling and heating.
Given a zone load, the model calculates the part-load ratio of the terminal unit such that the terminal unit’s “net” sensible capacity is equal to the zone load (if sufficient capacity is available). If it is determined that the part-load ratio of the zone terminal unit will be equal to 1, the DX cooling coil’s capacity is calculated in the same manner as described for single-speed DX cooling coils (ref: Coil:Cooling:DX:SingleSpeed). When it is determined that the part-load ratio of the zone terminal unit will be less than 1, the DX cooling coil’s capacity will be modulated through a reduction in refrigerant flow rate and an iterative solution technique will be used to calculate the performance of the DX cooling coil. For DX heating coils, capacity is calculated in the same manner as described for single-speed DX heating coils (ref: Coil:Heating:DX:SingleSpeed).
The “net” sensible full load cooling capacity is then compared to the zone sensible load. If the “net” sensible full load capacity is less than or equal to the absolute value of the zone sensible load, the DX coil operates at the maximum available capacity and, as a result, the zone air heat balance adjusts the zone air temperature. If the “net” sensible full load capacity is greater than the absolute value of the zone sensible load, an iterative solution technique is used to determine the total capacity required to meet the zone sensible load. This iteration loop entails successive modeling of DX coil performance and the loop iterates on the required total capacity until the operating “net” sensible capacity is equal to the zone sensible load.
Average Air Flow Calculations[LINK]
The variable refrigerant flow (VRF) terminal unit operates based on user-specified (or autosized) air flow rates. The VRF terminal unit’s supply air flow rate during cooling operation may be different than the supply air flow rate during heating operation. In addition, the supply air flow rate when no cooling or heating is required but the supply air fan remains ON can be different than the air flow rates when cooling or heating is required. The outside air flow rates can likewise be different in these various operating modes. The model takes these different flow rates into account when modeling the terminal unit, and the average air flow rate for each simulation time step is reported on the inlet/outlet air nodes of the various VRF terminal unit components in proportion to the calculated cycling ratio of the heat pump condenser. If the compressor does not cycle for a specific simulation time step then the heating or cooling air flow rate as specified by the user is assumed for the entire time step.
The average supply air and outdoor air mass flow rates through the terminal unit for the HVAC simulation time step are calculated based on the cycling ratio of the heat pump condenser as follows:
where:
CyclingRatio = cycling ratio of the heat pump condenser (heating or cooling)
The supply air and outside air flow rates when the DX cooling coil or the DX heating coil is ON are specified by the user (i.e., supply air volumetric flow rate during cooling operation, supply air volumetric flow rate during heating operation, outside air volumetric air flow rate during cooling operation, and outside air volumetric air flow rate during heating operation) and are converted from volumetric to mass flow rate. If the user has specified cycling fan/cycling coil operation (i.e. supply air fan operating mode schedule value is equal to 0), then the supply air and outside air mass flow rates when the coil is OFF are zero. If the user has specified constant fan/cycling coil operation (i.e. supply air fan operating mode schedule value is greater than 0), then the user-defined air flow rates when no cooling or heating is needed are used when the coil is OFF.
There is one special case. If the supply air fan operating mode schedule value specifies constant fan operation and the user also specifies that the supply air volumetric flow rate when no cooling or heating is needed is zero (or field is left blank), then the model assumes that the supply air and outside air mass flow rates when the coil is OFF are equal to the corresponding air mass flow rates when the cooling or heating coil was last operating (ON).
Calculation of Outlet Air Conditions[LINK]
When the supply air fan cycles on and off with the terminal unit coils (AUTO fan), the calculated outlet air conditions (temperature, humidity ratio, and enthalpy) from the DX heating coil or the DX cooling coil at full-load (steady-state) operation are reported on the appropriate coil outlet air node. The air mass flow rate reported on the air nodes is the average air mass flow rate proportional to the cycling ratio of the coil (see Average Air Flow Calculations above).
When the supply air fan operates continuously while the terminal unit coils cycle on and off (fan ON), the air mass flow rate reported on the air nodes is the average air mass flow rate proportional to the cycling ratio of the coil (see Average Air Flow Calculations above). Since the air flow rate can be different when the coil is ON compared to when the coil is OFF, then the average outlet air conditions from the DX heating coil or the DX cooling coil are reported on the appropriate coil outlet air node.
Calculation of Zone Heating and Cooling Rates[LINK]
At the end of each HVAC simulation time step, this compound object reports the heating or cooling rate and energy delivered to the zone. In terms of thermal energy delivered to the zone, the sensible, latent and total energy transfer rate to the zone is calculated as follows:
where:
hout,avg = enthalpy of the air being supplied to the zone, J/kg
The terminal unit’s energy transfer rate is used by the program in the zone air heat balance to determine the final zone air conditions. If the terminal unit is capable of meeting the zone thermostat set point temperature, then these report variables are indicative of the zone loads and may be compared directly to the report variables for predicted zone loads (ref: Output:Variable, e.g., Zone Predicted Sensible Load to Setpoint Heat Transfer Rate).
Since each of these energy transfer rates can be calculated as positive or negative values, individual reporting variables are established for cooling and heating and only positive values are reported. The following calculations are representative of what is done for each of the energy transfer rates:
IF ( < 0.0 ) THEN
< 0.0 ) THEN
ELSE
ENDIF
where:
In addition to heating and cooling rates, the heating and cooling energy supplied to the zone is also calculated for the time step being reported. The following example for total zone cooling energy is representative of what is done for the sensible and latent energy as well as the heating counterparts.
where:
TimeStepSys = HVAC system simulation time step, hr
Ventilated Slab[LINK]
Model Overview[LINK]
The input object ZoneHVAC:VentilatedSlab provides a model for ventilated slab systems that in general use outdoor air to “precool” slabs with colder nighttime air. This method of precooling the thermal mass of a space can be very effective when nighttime temperatures are low and the mass of the system is high enough to provide a significant amount of cooling potential during the day to counteract internal heat gains within a zone. Nearly all ventilated slabs are simple systems such as that shown in the right side of Figure 299. The fan is shown in a blow through position, but the model will allow either a blow or draw through configuration.
It should be noted that in Figure 299 the use of “unit ventilator” and “low temperature radiant system” do not imply that the user must also specify these elements in the input file. The ventilated slab model combines aspects of these two existing EnergyPlus features into a single model that the user specifies through the input shown in the Input/Output Reference.
The ventilated slab system has been implemented in a fashion that is similar to the “unit ventilator” system in EnergyPlus. The unit ventilator is a system that allows the user to bring in outdoor air (ventilation) that may or may not be tempered with a heating or cooling coil as shown the left side of Figure 299. The air can be delivered to the slab only (Figure 300), to the slab then to the space(Figure 301), and to several slabs in different areas in series (Figure 302). The model essentially combines the functionality of the low temperature radiant system (using air as a transport medium rather than water) and the unit ventilator. In some cases, the system may not meet all the zone heating and cooling load because it is operated not by setpoint of the zone but control temperature range and coil outlet air temperature set by user input. **Note that no coils are shown in Figure 302 for diagram simplicity but the implementation of the system shown in Figure 302 includes coils as in Figure 300 and Figure 301.
Connections to the Heat Balances[LINK]
The ventilated slab systems shown in the above diagrams connect or will connect to the various EnergyPlus heat balance equations in a variety of ways. All of the systems send outside or conditioned air through a slab or building element. This portion of the system acts in a fashion that is identical to the low temperature radiant systems. These surfaces that have the air being blown through them will impact the zone and air heat balances through the normal surface heat balances that interact with this surface. The ventilated slab will participate in the surface heat balances by exchanging radiation with other surfaces in the zone and in the air heat balances via convection to the zone air. So, the ventilated slab is handled identically to the low temperature radiant systems with respect to the zone and air heat balances. This information is valid for all three of the systems shown in the figures above.
For more information on the impact on the zone and air heat balances by the ventilated slab system, please consult the low temperature radiant system documentation and the EnergyPlus code.
CoolTower[LINK]
Overview[LINK]
The Cool Tower (object ZoneCoolTower:Shower) is available for modeling a cooltower (which is sometimes referred to as s wind tower or a shower cooling tower) which is a component that is intended to model a passive downdraught evaporative cooling (PDEC) that is designed to capture the wind at the top of a tower and cool the outdoor air using water evaporation before delivering it to a space. The air flow in these systems is natural as the evaporation process increases the density of the air causing it to fall through the tower and into the space without the aid of a fan. A cooltower typically consists of a water spray or an evaporative pad, a shaft, and a water tank or reservoir. Wind catchers to improve the wind-driven performance at the top of the tower are optional. Water is pumped over an evaporative device by water pump which is the only component consumed power for this system. This water cools and humidifies incoming air and then the cool, dense air naturally falls down through shaft and leaves through large openings at the bottom of cooltowers.
The shower cooling tower shown in figure below is controlled by a schedule and the specification of maximum water flow rate and volume flow rate as well as minimum indoor temperature. The actual flow rate of water and air can be controlled as users specify the fractions of water loss and flow schedule. The required input fields include effective tower height and exit area to obtain the temperature and flow rate of the air exiting the tower. A schedule and rated power for the water pump are also required to determine the power consumed. The component typically has a stand-alone water system that is not added to the water consumption from mains. However, users are required to specify the water source through an optional field, the name of water supply storage tank, in case any water comes from a water main.
The cooltower model employing a model of the inertial shower cooling tower is intended to establish the actual mass flow rate of the air that leaves the cooltower and the evaporation rate consumed during the processes within the cooltower. Like infiltration, ventilation, and earth tubes, the air is assumed to be immediately mixed with the zone air. The determination of simultaneous heat and mass transfer that occurs during natural evaporative cooling in cooltower is complicated. Therefore, some assumptions have been made to obtain the conditions of the air and water. All cooltowers are executed at the start of each time step called by HVAC manager, and the conditions of air temperature and humidity ratio in the zone will be corrected with any other air that enters the zone.
All temperatures in the following descriptions are in degrees C, mass flow rates are in kg/s, and volume flow rates are in m3/s.
Model Description[LINK]
The user must input the required information according to the Input Output Reference Manual (ref: ZoneCoolTower:Shower). The cooltower model requires a unique identifying name, an availability schedule, and the name of the zone being served. The schedule name must refer to a valid schedule type (range 0-1) and contain values of fractional cooltower operation as well as water pump operation. For the determination of the exit temperature and actual air volume flow rate, four additional inputs are required: effective tower height, exit area, fraction of flow schedule, and fraction of water loss. These define the conditions of the exit air, obtaining the conditions of outdoor air from the weather data and thus allow EnergyPlus to correct both the temperature and humidity level in the zone. The power consumed by the water pump can be directly determined by the schedule and rated power that the user inputs. The component is also controlled by the specification of minimum indoor temperature, maximum volume flow rate, and maximum water flow rate. These allow the model to prevent overcooling the zone or overestimation of the air volume flow rate. In addition, the user must input a flow control type according to the information that the user is able to obtain.
Simulation and Control[LINK]
The cooltower model first determines the temperature and volume flow rate of the exit air. Both parameters can be directly determined in case of water flow schedule control when the water flow rate is known. With the outdoor temperatures obtained from weather data, the exit air temperature (Tout) can be directly determined as functions of outdoor dry bulb temperature (DB), outdoor wet bulb temperature (WB), effective tower height (H) and water flow rate (WF) in l/min by using following equation.
The volume flow rate of the exit air (Q) can also be directly obtained as functions of water flow rate and effective tower height from the following equation.
In case of that the calculated air volume flow rate is greater than maximum air volume flow rate in this control, which leads to overestimation of actual volume flow rate of the exit air, the calculated air volume flow rate is replaced with the maximum.
For the simulation of wind-driven flow control where the water flow rate is unknown, the model determines velocity of the outlet air (Vout) as functions of effective tower height and wind speed of outdoor air (WS) as
The air volume flow rate (Q) is then calculated by
where A is opening area at the bottom of cooltower.
Substituting the air flow rate to the previous equation for Q, water flow rate is obtained as
Once water flow rate is determined, the model checks the limit of water flow rate that the user inputs, so that the model prevents overestimation of actual volume flow rate of the exit air. If the calculated water flow rate is greater than the maximum water flow rate, the maximum will be chosen. The model also replaces the calculated air volume flow rate with the maximum volume flow rate from the user input when the calculated is greater than the maximum. Then, the model calculates the air volume flow rate and exit temperature using the previous equation for Q and Tout.
This cooltower model allows the user to specify water loss due to drift or blow down and the loss of air flow (example: a cooltower which delivers air to both the interior and exterior of the building). If the user inputs the fraction of water loss or flow schedule that means some amount of the air actually goes to outside, the fractional values will be applied to previously calculated ones so that the model calculates both actual water flow rate (WFactual) and air volume flow rate (Qactual) as follows:
The model then determines the exit humidity ratio ( ) from the relation of mass balances below.
) from the relation of mass balances below.
In this case, actual mass flow rate at the inlet and outlet of cooltower cannot be correctly calculated with limited information. Thus, the model estimates initial conditions of the air based on the outdoor temperatures, the calculated exit air temperature, enthalpy of outdoor air (Hin) and outdoor barometric pressure (P). Assuming no enthalpy changes and pressure drops between inlet air and the initialized air, the humidity ratio and mass flow of the initialized air can be obtained by using EnergyPlus psychrometric functions and the following equation.
where and
and  are the humidity ratio and air density of the initialized air and
are the humidity ratio and air density of the initialized air and  is the humidity ratio of outdoor air.
is the humidity ratio of outdoor air.
Therefore, the humidity ratio of exit air, , is
, is
Once the humidity ratio at the exit is determined, the model can obtain the actual density ( ), specific heat (
), specific heat ( ), and mass flow rate (
), and mass flow rate ( ) of the air leaving cooltower by using EnergyPlus psychrometric function and following equation.
) of the air leaving cooltower by using EnergyPlus psychrometric function and following equation.
Assuming that the water temperature equals to outdoor wet bulb temperature, the model eventually determines density of the water and evaporation rate as bellows.
Earthtube[LINK]
The earth tube model (input object ZoneEarthtube) provides a simple earth tube model that uses a complex ground heat transfer model to establish the temperature of the soil at the depth of the earth tube. The following information defines the basis for the model including the assumptions and mathematical equations. It supplements the information for the ZoneEarthtube input object given in the Input/Output Reference for EnergyPlus.
Input Requirement
Pipe : Pipe radius(m), Pipe thickness(m), Pipe length(m)
Air velocity inside pipe(m/s), Depth of the radial center of pipe below ground (m)
Soil : Soil density(kg/m3), Soil specific heat(J/kg°C),
Fraction of evaporation rate
Assumption(s)
Pipe has uniform cross section area at axial direction.
Wind velocity (m/s), u, is the annual average value. This is calculated from EnergyPlus weather data by averaging individual wind velocity values of the whole year. The convective heat transfer coefficient at the soil surface (W/m2°C), hs, is function of wind speed u. According to McAdams(1954) hs can be approximated by the following correlation (Krarti, 1995).
In case of he and hr, they can be determined by the following equations.
with a = 103 Pa/°C.
Average air temperature (°C), Tma, is also calculated from EnergyPlus weather data by averaging individual air temperature values of the whole year.
The appropriate value of hemispherical emittance of the ground surface, ε, is 0.93~0.96. Radiation constant (W/m2), ΔR, depends on soil radiative properties, air relative humidity, and effective sky temperature. An appropriate value of ΔR according to Krarti (1995) is 63 W/m2.
The absorption coefficient, β, depends on the soil absorptance and shading condition. The coefficient β is approximately equal to one minus the soil surface albedo. Albedo depends on soil cover and moisture content. Albedo=0.1 corresponds to wet soils, albedo=0.2 to moderate soils, and albedo=0.3 to dry soils.
Average solar radiation (W/m2), Sm, is determined from EnergyPlus weather data by averaging individual global horizontal solar radiation values of the whole year.
The fraction of evaporation rate, f, also depends mainly on the soil cover and the soil moisture level. Based on the results reported by Penman, it is recommended to estimate the fraction f as follows. For bare soil, f is directly proportional to soil moisture content. For instance, f=1 corresponds to saturated soils, f=0.6~0.8 to wet soils, f=0.4~0.5 to moist soils, f=0.1~0.2 to arid soils. For dry soils, f = 0, since no evaporation occurs. For covered soils, the fraction f is obtained by multiplying 0.7 by the value of f for bare soil depending on the soil moisture content (Krarti, 1995).
Relative humidity, ra, is also calculated from EnergyPlus weather data by averaging individual relative humidity values of the whole year.
The soil thermal diffusivity (m2/s), αs, and conductivity (W/m°C), ks, varies with the density and moisture content. According to the 1991 ASHRAE Handbook of HVAC Applications (Table 4, pp. 11.4), the following values are recommended under different conditions.
Annual angular frequency, w, is equal to 1.992 x 10-7rad/s, and dampening depth (m), D, is calculated from the following equation:
The value of δ is evaluated as follows.
Amplitude of the air temperature (°C), Tva, can be evaluated from EnergyPlus weather data by dividing the difference between the maximum and minimum air temperature value of the whole year by two. Similarly, amplitude of the solar radiation (W/m2), Sv, can also be determined from weather data by dividing the difference between the maximum and minimum solar radiation value of the whole year by two.
Phase angle between the insolation and the air temperature (rad), φI , is calculated by subtracting insolation phase angle from air temperature phase angle. Phase angle of insolation and air temperature is the point from the beginning of the year at which the insolation and air temperature respectively reaches the minimum value among the whole year.
Phase constant of the air (sec), t0a, is the time elapsed from the beginning of the year at which the air temperature reaches the minimum value in the year.
By using all the input parameters and variables described above, average soil surface temperature (°C), Tm, amplitude of the soil surface temperature variation (°C), As, phase constant of the soil surface (sec), t0, and phase angle difference between the air and soil surface temperature (rad), Φs, can be evaluated as follows 1):
(Note: Tm, As, and t0 are calculated by the CalcSoilSurfTemp program and are inputs to EnergyPlus. The remainder of this section describes what has been implemented in EnergyPlus.)
The symbols || || and Arg denote the modulus and the argument of a complex number respectively. In order to calculate As and Φs, the complex number under consideration can be rearranged as the following form:
Assuming a homogeneous soil of constant thermal diffusivity, the temperature at any depth z and time t can be estimated by the following expression 2).
In this expression, the unit of time, t, and phase constant of the soil surface, t0, should be converted into days. Similarly, the unit of soil thermal diffusivity, αs, should also be converted into m2/days.
By integrating the expression with respect to depth, the average temperature of a vertical soil profile ranging between depth z1and z2 (°C ) can be determined as follows 2).
where,
As the final step with regard to the heat transfer between soil and earth tube system, thermal conductivity of air (W/m°C), kair, and kinetic viscosity of air (m2/s), υ, should calculated first 3).
By using the values of thermal conductivity of air, kair, and kinetic viscosity of air, υ, the convective heat transfer coefficient at the inner pipe surface (W/m2°C), hc, can be evaluated. It is a function of Reynolds number, Re, and Nusselt number, Nu 4), where
where r1 is inner pipe radius (m), and Va is average pipe air velocity (m/s).
After determining the convective heat transfer coefficient, Rc, Rp and Rs are respectively calculated as follows.
where Rc is thermal resistance due to convection heat transfer between the air in the pipe and the pipe inner surface (m-C/W), Rp is thermal resistance due to conduction heat transfer between the pipe inner and outer surface (m-C/W), and Rs is thermal resistance due to conduction heat transfer between the pipe outer surface and undisturbed soil (m-C/W). In addition r2 is pipe thickness (m), r3 is distance between the pipe outer surface and undisturbed soil (m), and L is pipe length (m).
Finally, the heat transfer between the soil and the air inside the pipe is equal to the amount of heat losses as air flows along the pipe (Jacovides and Mihalakakou, 1995).
with
where Ut is overall heat transfer coefficient of the whole earth tube system (W/C-m), Ta(y) is air temperature of the pipe at the distance y from the pipe inlet (°C), and ma is mass flow rate of ambient air through pipe (kg/s). Ca is specific heat of air (J/kg°C) and Rt is total thermal resistance between pipe air and soil (m-C/W).
Initial condition of inlet air temperature is equal to the ambient air temperature. Outlet air temperature is finally evaluated by solving the heat transfer equation above.
Table: Nomenclature for Earthtube Model
Variable|Description|Units ——–|———–|—– As amplitude of the soil surface temperature variation (°C)
Ca specific heat of air (J/kg°C)
hc convective heat transfer coefficient at the inner pipe surface (W/m2°C)
hs convective heat transfer coefficient at the soil surface (W/m2°C)
kair thermal conductivity of the air (W/m°C)
kp pipe thermal conductivity (W/m°C)
ks soil thermal conductivity (W/m°C)
L pipe length (m)
ma mass flow rate of ambient air through pipe (kg/s)
ra relative humidity
Rc thermal resistance due to convection heat transfer between the air in the pipe and the pipe inner surface (m-C/W)
Rp thermal resistance due to conduction heat transfer between the pipe inner and outer surface (m-C/W)
Rs thermal resistance due to conduction heat transfer between the pipe outer surface and undisturbed soil (m-C/W)
Rt total thermal resistance between pipe air and soil (m-C/W)
ΔR radiation constant (63W/m2)
r1 inner pipe radius (m)
r2 pipe thickness (m)
r3 distance between the pipe outer surface and undisturbed soil (m)
Sm average solar radiation (W/m2)
Sv amplitude of the solar radiation (W/m2)
t time elapsed from beginning of calendar year (days)
Ta(y) air temperature of the pipe at the distance y from the pipe inlet (°C)
Tm average soil surface temperature (°C)
Tma average air temperature (°C)
t0 phase constant of the soil surface (sec; days)
t0a phase constant of the air (sec; days)
Tva amplitude of the air temperature (°C)
Tz,t~~ ground temperature at time t and depth z (°C)
Tz1,z2,t~~ soil profile temperature at time t, averaged over depths between z1 and z2 (°C)
u wind velocity above the ground surface (m/s)
Ut overall heat transfer coefficient of the whole earth tube system (W/m-C)
Va average pipe air velocity (m/s)
z depth of the radial center of pipe below soil surface (m)
z1 upper bounds of some vertical profile in soil (m)
z2 lower bounds of some vertical profile in soil (m)
αs soil thermal diffusivity (m2/s; m2/days)
β soil absorption coefficient (= 1 – soil albedo)
ε hemispherical emittance of the ground surface
φI phase angle between the insolation and the air temperature (rad)
Φs phase angle difference between the air and soil surface temperature (rad)
υ kinetic viscosity of air (m2/s)
w annual angular frequency (=1.992 x 10-7rad/s)
References[LINK]
Krarti M., Lopez-Alonzo C., Claridge D. E. and Kreider J. F. 1995. Analytical model to predict annual soil surface temperature variation. Journal of Solar Energy Engineering 117, 91~99
Labs K. In: Cook J., editor. 1989. Passive cooling. Cambridge Massachusetts, London, England: MIT Press
Al-Ajmi F., Loveday D. L. and Hanby V. I. 2005. The Cooling Potential of Earth-air Heat Exchangers for Domestic Buildings in a Desert Climate, Building and Environment
Necati Ozisik M. 1885. Heat transfer: A basic approach, McGraw-Hill Book Company
Jacovides C. P. and Mihalakakou G. 1995. An Underground Pipe Systems as an Energy Source for Cooling/Heating Purposes. Renewable Energy 6, pp.893~900
Thermal Chimney Model[LINK]
The ZoneThermalChimney input object is available for modeling a thermal chimney which is a device that uses stack driven air movement to ventilate spaces within a building. These systems have been used successfully in buildings as small as the size of an outhouse up to large commercial buildings. The air within a thermal chimney is heated naturally using solar energy. The air increases in temperature which causes its density to drop. This drop in density results in a natural vertical movement of air and a local drop in pressure. The drop in pressure is relieved by drawing air from the building interior, and the heat gained within the thermal chimney does not enter the occupied portion of the building. These systems are often used in support of natural ventilation systems. The EnergyPlus model will seek to model the air heat balance effects of the thermal chimney, balance air movements caused by the thermal chimney, and report other appropriate system variables. The new model will be linked into the air heat balance in a fashion similar to the current infiltration and simple ventilation models but will not be linked to an HVAC air loop. Any flow through the thermal chimney will be accounted for in the air mass balance in the HVAC calculations. However, other sophisticated ventilation strategies can be handled by other existing EnergyPlus components.
Thermal Chimney Input Requirements
Cross sectional areas of each air channel inlet (m2)
Assumptions
The discharged amount of interior air induced by the thermal chimney is replaced by the outdoor air infiltration.
Mathematical model currently available for thermal chimneys has the capability to handle the thermal chimney having only one inlet. In other words, it is unlikely that thermal chimneys with multiple inlets due to multiple stories utilizing the common thermal chimney can be mathematically modeled without computational fluid dynamics. Therefore, if the thermal chimney to be modeled has multiple inlets, it will be assumed that it will have only one inlet. For this assumption, the user will be required to specify the relative ratio of air flow rates passing through each inlet to compute the overall length of the thermal chimney (m), L, overall room air temperature (K), Tr, and overall cross sectional area of air channel inlet (m2), Ai, as follows:
Where, Ain is the cross sectional area of nth air channel inlet (m2), Ln is the distance from the top of thermal chimney to nth inlet (m), En is the room air specific enthalpy corresponding to nth inlet (J/kg), rn is the relative ratio of air flow rate passing through nth inlet and Trn is the room air temperature corresponding to nth inlet (K). Among them, room air specific enthalpy, En, and room air temperature corresponding to each inlet, Trn, are directly calculated inside EnergyPlus. In addition, the relative ratios should meet the following expression:
After merging the multiple inlets into a single inlet condition based on the description above, the following algorithm which is widely used is employed for the modeling of the thermal chimney.
The key output parameter in the thermal chimney model is the enhanced amount of natural ventilation rate caused by the presence of a thermal chimney. In order to determine the enhanced ventilation, the discharge air temperature from a thermal chimney should be calculated, which, in turn, should be computed based on the information on the absorber wall temperature, glass cover temperature and the vertical air temperature distribution within the thermal chimney. Among them, energy balances for the absorber wall and the glass cover are carried out using the existing algorithm currently available in EnergyPlus, which has the similar approach to the Trombe wall. On the other hand, the vertical air temperature distribution and the resultant discharge air temperature of the thermal chimney are computed using the separate thermal chimney algorithm described in the following paragraphs.
Once the glass cover temperature and the absorber wall temperature are computed using the existing modeling algorithm in EnergyPlus, the energy balance for the fluid (air inside the thermal chimney) can be expressed as:
Where, m is the total mass flow rate of the air (kg/s), Cp is the specific heat of air (J/kg°C), w is the width of the absorber wall (m) and x is the elemental length of the absorber wall (m).
Since the initial condition of inlet air temperature in this differential equation is equal to the room air temperature (i.e. x = 0, Tf,i = Tr), the outlet air temperature, Tfo, can be finally evaluated.
Finally, the total air flow rate caused by the thermal chimney (m3/s), Q, can be evaluated from the following expression [1]:
Where, Cd is the discharge coefficient, Ao and Ai is the cross sectional areas of air channel outlet and inlet (m2), respectively, Tfo is the outlet air temperature (K), Tr is the room air temperature (K) and L is the total length of the thermal chimney (m).
Since multiple inlets are merged into a single inlet in the beginning, the air flow rate passing through each inlet due to the existence of the thermal chimney can be finally determined as follows:
Where, Qn is the air flow rate passing through nth inlet (m3/s) and rn is the relative ratio of air flow rate passing through nth inlet.
The discharged amount of interior air from each zone caused by the presence of the thermal chimney is assumed to be replaced by the outdoor air infiltration.
References[LINK]
N. K. Bansal, R. Mathur and M. S. Bhandari, Solar Chimney for enhanced Stack Ventilation, Building and Environment, 28, pp.373-377, 1993
K. S. Ong, A Mathematical Model of a Solar Chimney, Renewable Energy, 28, pp.1047-1060, 2003
N. K. Bansal, R. Mathur and M. S. Bhandari, A Study of Solar Chimney Assisted Wind Tower System for Natural Ventilation in Buildings, Building and Environment, 29, pp.495-500, 1994
J. Marti-Herrero and M. R. Heras-Celemin, Dynamic Physical Model for a Solar Chimney, Solar Energy, 81, pp. 614-622, 2007
M. M. Aboulnaga and S. N. Abdrabboh, Improving Night Ventilation into Low-rise Buildings in Hot-arid Climates Exploring a Combined Wall-roof Solar Chimney, Renewable Energy, 19, pp. 47-54, 2000
Zone Outdoor Air Unit[LINK]
The zone outdoor air unit (object ZoneHVAC:OutdoorAirUnit) is intended to model systems such as zone make-up air units and dedicated outside air systems. These components are “zone equipment” meaning that they do not require an air loop but serve a zone directly. The system is comprised of a supply fan (in either draw through or blow through configuration), an optional exhaust fan, and a variety of components such as heating coils, cooling coils, heat recovery, etc. The object of the zone outdoor air unit is to bring in additional ventilation air into a zone. These might be used for high ventilation spaces such as kitchens or laboratories where another system is primarily responsible for space conditioning while the zone outside air unit is primarily responsible for fresh air delivery to the zone. Most of the information necessary to configure a zone outdoor air unit is contained in the EnergyPlus Input/Output Reference. A diagram of the zone outdoor air unit is shown below. As this system is relatively simple and does not contain any unique operating algorithm or equations, the discussion here is limited to the application of the user defined controls and how it relates to the operation of the device.
Controls[LINK]
Three input parameters control the operation of the zone outdoor air unit. The unit control type has two options: neutral or temperature. If the temperature control type is selected, the user must also provide a high and low air temperature control schedule. The algorithm for controlling the zone outdoor air unit is dependent on these parameters which are used as described below.
Neutral Control. If the user selects neutral control, the intent is to provide additional outside air to the zone without imposing any additional thermal load on the zone or any other systems serving the zone. In other words, the unit will attempt to provide air to the zone at the zone mean air temperature. Mathematically, this means:
where:
Tout = the outlet temperature of the zone outdoor air unit
TMAT = the mean air temperature of the zone being served by the unit
It should be noted that to avoid excessive iteration that the zone mean air temperature that is used is the mean air temperature from the previous time step. This will result in a slight lagging that may introduce a slight thermal load, but this should be minimal.
Temperature Control. If the user selects temperature control, the intent is to limit the outlet temperature of the unit for either heating or cooling or both or perhaps to provide unconditioned air to the space. The algorithm used to determine the outlet temperature of the unit is as follows. When the outdoor air temperature is at or below the low air temperature control schedule value, the outlet temperature is set to the low air temperature control schedule value and any heating equipment included in the unit description and available will attempt to provide enough heating to produce an outlet temperature equal to the low temperature schedule value. When the outdoor air temperature is at or above the high air temperature control schedule value, the outlet temperature of the unit is set to the high air temperature control schedule value and any cooling equipment included in the unit description and available will attempt to provide enough cooling to produce an outlet air temperature equal to the high temperature schedule value. When the outdoor air temperature is between the high and low temperature values, the unit will not provide any conditioning of outdoor air and will simply deliver it to the zone. Mathematically, this can be summarized as:
where:
Tout = the outlet temperature of the zone outdoor air unit
Toa = the outside air temperature
Thigh = the high control air temperature schedule value
Tlow = the low control air temperature schedule value
If the user wishes to provide “unconditioned” air all of the time, the high and low control temperature values can be set very high and very low, respectively, to always force the unit to provide unconditioned air. The same effect can also be realized by not specifying any conditioning components (such as coils) in the unit. The user can also limit the device to cooling only by specifying a low control temperature schedule with extremely low values. Conversely, the user can limit the device to heating only by specifying a high control temperature schedule with extremely high values. The user can also limit the equipment specified as part of the device to either cooling or heating components to get similar effects. In essence, the temperature control provides a variety of options in a single control type through the use of the high and low control temperature schedules.
Zone Exhaust Fan[LINK]
The zone exhaust fan (Fan:ZoneExhaust) is a simple model to account for the fan electric energy use and impact on central air handlers from bathroom and hood exhaust. Because the fan only extracts air from the zone, it doesn’t directly impact the zone itself.
The fan flow rate is either constant or variable depending on if the user input a flow fraction modifier schedule. The value entered for maximum volume flow rate is converted to a design mass flow rate using standard (altitude-adjusted) density and used as the design flow rate. If a flow fraction schedule is used, then its values, fFract, are multiplied by the design flow rate to obtain the current mass flow.
The exhaust fan model is similar to, but simpler than, the models used for air system fans. The electric power calculation is simplified and uses a constant overall efficiency. All of the fan power is added to the air stream.
The controls for determining if the the exhaust fan will operate can be based on a number of factors including: an on/off availability schedule, interaction with system availability managers, minimum zone air temperature control limits and a variable flow fraction schedule. When the fan is coupled to the system availability managers then it will operate if either the local availability schedule or the system availability manager’s indicate that the fan should run. When the fan is not coupled to the system availability manager, then it only uses the local availability schedule and ignores availability managers. If using the flow fraction schedule and the resulting flow is zero, then fan will not run. If using the minimum zone temperature limit schedule then the fan will only run if the fan inlet temperature is warmer than the limit.
The exhaust fan’s interaction with the air system depends on the value, fBal, of the schedule for the fraction of the exhaust that is balanced. The model tracks the exhaust flows in two ways, balanced and unbalanced. Balanced exhaust air flow is considered to have been made up from simple airflow from infiltration, ventilation or zone mixing. Unbalanced exhaust air flow is considered to not be balanced by simple air flows and needs to be balanced by the air system operation. Both of these types of flow are summed at the zone and whole air system level. In a zone, the return air node flow rate is reduced from what it would be with no exhaust by the portion of the zone’s exhaust flow that is unbalanced. In an air handler with an outdoor air system, the outdoor air flow rate may be increased so as to be sufficient to provide all the unbalanced exhaust air for all the zones on the air handler (when possible).
Documentation content copyright © 1996-2014 The Board of Trustees of the University of Illinois and the Regents of the University of California through the Ernest Orlando Lawrence Berkeley National Laboratory. All rights reserved. EnergyPlus is a trademark of the US Department of Energy.
This documentation is made available under the EnergyPlus Open Source License v1.0.